题目内容
2.如图(a),半径为r1的圆形区域存在垂直纸面向里的匀强磁场B,在垂直于磁场的平面内,阻值为R2、长为r2的金属杆OQ绕端点O转动,杆的末端Q通过电刷与圆形金属环保持良好接触. O点、圆环与一个电路连接,P是加上正向电压才能导通的理想元件.a、b端点通过导线与水平放置的两平行金属板相连.用电压传感器(内阻足够大)测得a、b两端的电压U与金属杆角速度ω的关系如图(b)所示,ω>0代表圆盘逆时针转动.已知:R1=3R2,r1=0.40m,r2=0.50m,两金属板间距离d=1cm,导线的电阻忽略不计.

(1)根据图(b)写出OA、OB段对应U与ω的关系式
(2)求圆形区域内匀强磁场磁感应强度B大小;
(3)若一质量m=1.2×10-6kg、带电量q=-1.0×10-8C的粒子,以初速v0=4m/s沿两板正中间水平射入金属板间,并能沿直线从金属板右边穿出,求金属杆的角速度ω.(设粒子穿越电场过程中金属杆匀速转动,重力加速度为g取10m/s2).
分析 (1)OA段、OB段都是正比例图象,求解出斜率即可;
(2)当角速度为100rad/s时,电压为6V,根据切割公式E=BL$\overline{v}$和$\overline{v}$=$ω•\frac{L}{2}$得到E=$\frac{1}{2}B{L}^{2}$ω列式分析;
(3)粒子能沿直线从金属板右边穿出,受重力和电场力平衡,得到电场力向上,结合右手定则判断杆的转动方向;根据平衡条件和法拉第电磁感应定律列式分析.
解答 解:(1)oa段:U=0.06ω(ω>0),
ob段:U=0.1ω(ω<0);
(2)当OQ顺时针旋转时,P不导通,a、b两端的电压等于感应电动势;由法拉第电磁感应定律:U=$\frac{1}{2}$Br12ω
当U=6V时,角速度ω=100rad/s,解得:B=$\frac{2U}{{r}_{1}^{2}ω}$=$\frac{2×6}{0.{4}^{2}×100}$=0.75T;
(3)粒子能沿直线从金属板右边穿出,说明其所受电场力方向竖直向上,板间场强方向竖直向下.说明OQ沿逆时针方向旋转;
粒子所受电场力与重力平衡:Eq=mg,
根据法拉第电磁感应定律,有:Ed=$\frac{1}{2}$Br12ω,
联立解得角速度:ω=200rad/s;
答:
(1)OA段对应U与ω的关系式为U=0.06ω(ω>0),OB段对应U与ω的关系式为U=0.1ω(ω<0);
(2)圆形区域内匀强磁场磁感应强度B大小为0.75T;
(3)金属杆的角速度ω为200rad/s.
点评 本题是力电综合问题,关键是明确二极管具有单向导电性,杆转动切割时感应电动势为E=BL$\overline{v}$,不难.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.一质量为10千克的物体,受到大小分别为2N、4N、5N的作用,其合力最小为多少牛( )
| A. | 3N | B. | 11N | C. | 0N | D. | 无法确定 |
13.关于重力的说法正确的是:( )
| A. | 若一个物体的质量分布发生变化,其重心位置可能会发生变化 | |
| B. | 重力的方向一定垂直于接触面 | |
| C. | 一质量分布均匀的砖块,平放、侧放和立放时,其重心在砖内的位置一定变化 | |
| D. | 只有静止的物体才会受到重力作用 |
10. 一列简谐横波沿x轴传播,某时刻波形如图所示,此时质点F的运动方向向y轴负方向,则( )
一列简谐横波沿x轴传播,某时刻波形如图所示,此时质点F的运动方向向y轴负方向,则( )
 一列简谐横波沿x轴传播,某时刻波形如图所示,此时质点F的运动方向向y轴负方向,则( )
一列简谐横波沿x轴传播,某时刻波形如图所示,此时质点F的运动方向向y轴负方向,则( )| A. | 质点E的振幅为零 | B. | 此波向x轴正方向传播 | ||
| C. | 质点C此时向y轴负方向运动 | D. | 质点C将比质点B先回到平衡位置 |
7. 如图所示,一个边长为L的正方形abcd,它是磁感应强度为B的匀强磁场横截面的边界线.一带电粒子从ad边的中点O垂直于磁场方向射入其速度方向与ad边成θ=30°角,如图,已知该带电粒子所带电荷量为+q质量为m,重力不计,则( )
如图所示,一个边长为L的正方形abcd,它是磁感应强度为B的匀强磁场横截面的边界线.一带电粒子从ad边的中点O垂直于磁场方向射入其速度方向与ad边成θ=30°角,如图,已知该带电粒子所带电荷量为+q质量为m,重力不计,则( )
 如图所示,一个边长为L的正方形abcd,它是磁感应强度为B的匀强磁场横截面的边界线.一带电粒子从ad边的中点O垂直于磁场方向射入其速度方向与ad边成θ=30°角,如图,已知该带电粒子所带电荷量为+q质量为m,重力不计,则( )
如图所示,一个边长为L的正方形abcd,它是磁感应强度为B的匀强磁场横截面的边界线.一带电粒子从ad边的中点O垂直于磁场方向射入其速度方向与ad边成θ=30°角,如图,已知该带电粒子所带电荷量为+q质量为m,重力不计,则( )| A. | 粒子恰好不从cd边射出,轨道半径最大值为L | |
| B. | 粒子从ab边射出区域的最大长度为$\frac{2}{3}$L | |
| C. | 粒子恰好没有从ab边射出,该带电粒子在磁场中飞行的时间为$\frac{3πm}{5Bq}$ | |
| D. | 带电粒子从ad边射出,粒子入射时的最大速度为$\frac{BqL}{3m}$ |
14.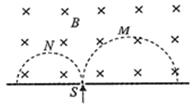 2016年3月10日,我国科学家宣布利用超强超短激光成功产生了反物质,现将正电子、负电子以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,不计粒子的重力,下列表述正确的是( )
2016年3月10日,我国科学家宣布利用超强超短激光成功产生了反物质,现将正电子、负电子以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,不计粒子的重力,下列表述正确的是( )
 2016年3月10日,我国科学家宣布利用超强超短激光成功产生了反物质,现将正电子、负电子以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,不计粒子的重力,下列表述正确的是( )
2016年3月10日,我国科学家宣布利用超强超短激光成功产生了反物质,现将正电子、负电子以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,不计粒子的重力,下列表述正确的是( )| A. | N为负电子,M为正电子 | B. | N的速率小于M的速率 | ||
| C. | 洛伦兹力对M做正功、对N做负功 | D. | M的运行时间大于N的运行时间 |
12. 如图所示,从炽热的金属丝漂出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )
如图所示,从炽热的金属丝漂出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )
 如图所示,从炽热的金属丝漂出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )
如图所示,从炽热的金属丝漂出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )| A. | 将偏转电场极性对调 | B. | 减小偏转电极间的距离 | ||
| C. | 增大偏转电极间的电压 | D. | 减小偏转电极间的电压 |
 (1)“测定玻璃折射率”的实验中,在玻璃砖的一侧竖直插两个大头针A、B.在另一侧再竖直插两个大头针C、D,在插入第四个大头针D时,要使它挡住大头针D与大头针A、B的像,如图1在白纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边,根据该图用直尺画出光路图,并说明所要测量的物理量(用符号和文字说明)入射角i与折射角r,并据此写出求玻璃砖的折射率的表达式n=$\frac{sini}{sinr}$.
(1)“测定玻璃折射率”的实验中,在玻璃砖的一侧竖直插两个大头针A、B.在另一侧再竖直插两个大头针C、D,在插入第四个大头针D时,要使它挡住大头针D与大头针A、B的像,如图1在白纸上留下的实验痕迹,其中直线a、a′是描在纸上的玻璃砖的两个边,根据该图用直尺画出光路图,并说明所要测量的物理量(用符号和文字说明)入射角i与折射角r,并据此写出求玻璃砖的折射率的表达式n=$\frac{sini}{sinr}$.