题目内容
12. 如图所示,竖直放置的绝热圆柱形容器内用绝热活塞封闭一定质量的理想气体,已知容器横截面积为S,活塞重为G1,与容器底部相距h,大气压强为p0,现通过电热丝缓慢加热气体,当气体的温度为T1时活塞上升了$\frac{h}{2}$,此时停止对气体加热,同时在活塞上缓慢添加砂粒,当添加砂粒的重为G0时,活塞恰好回到原来位置,不计摩擦,求此时气体的温度.
如图所示,竖直放置的绝热圆柱形容器内用绝热活塞封闭一定质量的理想气体,已知容器横截面积为S,活塞重为G1,与容器底部相距h,大气压强为p0,现通过电热丝缓慢加热气体,当气体的温度为T1时活塞上升了$\frac{h}{2}$,此时停止对气体加热,同时在活塞上缓慢添加砂粒,当添加砂粒的重为G0时,活塞恰好回到原来位置,不计摩擦,求此时气体的温度.
分析 以缸内气体为研究对象,温度为${T}_{1}^{\;}$时,根据活塞平衡求出气体的压强;末态时根据活塞受力平衡求出压强,根据理想气体状态方程即可求出末态温度;
解答 解:开始时气体的压强为${p}_{1}^{\;}$,由平衡可知:${p}_{1}^{\;}S={G}_{1}^{\;}+{P}_{0}^{\;}S$
活塞恰好回到原来位置的压强为${p}_{2}^{\;}$,由活塞平衡知:
${p}_{2}^{\;}S=({G}_{1}^{\;}+{G}_{0}^{\;})+{p}_{0}^{\;}S$
温度为${T}_{1}^{\;}$时,气体的体积为:${V}_{1}^{\;}=\frac{3}{2}hS$
温度为${T}_{2}^{\;}$时,气体的体积为:${V}_{2}^{\;}=hS$
由理想气体状态方程可得:$\frac{{p}_{1}^{\;}{V}_{1}^{\;}}{{T}_{1}^{\;}}=\frac{{p}_{2}^{\;}{V}_{2}^{\;}}{{T}_{2}^{\;}}$
联立方程得:${T}_{2}^{\;}=\frac{2({G}_{1}^{\;}+{G}_{0}^{\;}+{p}_{0}^{\;}S){T}_{1}^{\;}}{3({G}_{1}^{\;}+{p}_{0}^{\;}S)}$
答:此时气体的温度$\frac{2({G}_{1}^{\;}+{G}_{0}^{\;}+{p}_{0}^{\;}S){T}_{1}^{\;}}{3({G}_{1}^{\;}+{p}_{0}^{\;}S)}$.
点评 本题考查理想气体状态方程的应用,关键是确定初末各状态参量,温度是热力学温度,注意压强的求解采用力平衡法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.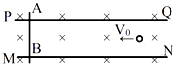 如图所示为某一装置的俯视图,PQ、MN为水平放置且足够长的平行金属薄板,两板间有磁感应强度为B的匀强磁场,方向垂直薄板平面向里,金属棒AB垂直放置在两板上且与两板接触良好.现有质量为m,电荷量为+q的粒子以初速度V0水平向左射入两板之间,若磁场足够大,粒子的重力不计,且粒子不会打到两板上,则( )
如图所示为某一装置的俯视图,PQ、MN为水平放置且足够长的平行金属薄板,两板间有磁感应强度为B的匀强磁场,方向垂直薄板平面向里,金属棒AB垂直放置在两板上且与两板接触良好.现有质量为m,电荷量为+q的粒子以初速度V0水平向左射入两板之间,若磁场足够大,粒子的重力不计,且粒子不会打到两板上,则( )
 如图所示为某一装置的俯视图,PQ、MN为水平放置且足够长的平行金属薄板,两板间有磁感应强度为B的匀强磁场,方向垂直薄板平面向里,金属棒AB垂直放置在两板上且与两板接触良好.现有质量为m,电荷量为+q的粒子以初速度V0水平向左射入两板之间,若磁场足够大,粒子的重力不计,且粒子不会打到两板上,则( )
如图所示为某一装置的俯视图,PQ、MN为水平放置且足够长的平行金属薄板,两板间有磁感应强度为B的匀强磁场,方向垂直薄板平面向里,金属棒AB垂直放置在两板上且与两板接触良好.现有质量为m,电荷量为+q的粒子以初速度V0水平向左射入两板之间,若磁场足够大,粒子的重力不计,且粒子不会打到两板上,则( )| A. | 若带电粒子做匀速直线运动,则金属棒AB应向右运动 | |
| B. | 金属棒的速度为2 V0时,带电粒子可能做匀速直线运动 | |
| C. | 若金属棒的向左运动速度也为V0,则带电粒子一定做匀速直线运动 | |
| D. | 若金属棒一直未动,则带电粒子从初始时到位移大小为$\frac{m{V}_{0}}{qB}$时的时间间隔可能为t=$\frac{5πm}{3qB}$ |
7. 如图,M、N、Q是匀强电场中的三点,MN垂直于NQ,MN=4cm,NQ=3cm,MQ与电场方向平行,M,N两点的电势分别为5V和1.8V.则电场强度大小和Q点的电势分别为( )
如图,M、N、Q是匀强电场中的三点,MN垂直于NQ,MN=4cm,NQ=3cm,MQ与电场方向平行,M,N两点的电势分别为5V和1.8V.则电场强度大小和Q点的电势分别为( )
 如图,M、N、Q是匀强电场中的三点,MN垂直于NQ,MN=4cm,NQ=3cm,MQ与电场方向平行,M,N两点的电势分别为5V和1.8V.则电场强度大小和Q点的电势分别为( )
如图,M、N、Q是匀强电场中的三点,MN垂直于NQ,MN=4cm,NQ=3cm,MQ与电场方向平行,M,N两点的电势分别为5V和1.8V.则电场强度大小和Q点的电势分别为( )| A. | 100V/m和1V | B. | 80V/m和0 | C. | 100V/m和0 | D. | 80V/m和1V |
17. 如图为蹦床比赛某运动员从高处下落到蹦床后又被弹回原高度过程中的速度随时间变化的图象,0~t1时段和t7~t8间段图线为直线,若时0~t8时间内相邻时刻时间间隔相等,则( )
如图为蹦床比赛某运动员从高处下落到蹦床后又被弹回原高度过程中的速度随时间变化的图象,0~t1时段和t7~t8间段图线为直线,若时0~t8时间内相邻时刻时间间隔相等,则( )
 如图为蹦床比赛某运动员从高处下落到蹦床后又被弹回原高度过程中的速度随时间变化的图象,0~t1时段和t7~t8间段图线为直线,若时0~t8时间内相邻时刻时间间隔相等,则( )
如图为蹦床比赛某运动员从高处下落到蹦床后又被弹回原高度过程中的速度随时间变化的图象,0~t1时段和t7~t8间段图线为直线,若时0~t8时间内相邻时刻时间间隔相等,则( )| A. | t3、t5时刻运动员处于失重状态 | |
| B. | t6时刻运动员重力势能最小,蹦床弹性势能最大 | |
| C. | t2时刻运动员受力平衡,运动员动能最大 | |
| D. | t1、t7时刻运动员速度相同 |
1. 如图所示,理想变压器输入交变电压u=220$\sqrt{2}$sin100πt(V),理想变压器原、副线圈匝数比为2:1,已知电水壶额定功率为880W,排气扇机内电阻为1Ω,电流表示数为18A,各用电器均正常工作.电流表为理想电表.下列说法正确的是( )
如图所示,理想变压器输入交变电压u=220$\sqrt{2}$sin100πt(V),理想变压器原、副线圈匝数比为2:1,已知电水壶额定功率为880W,排气扇机内电阻为1Ω,电流表示数为18A,各用电器均正常工作.电流表为理想电表.下列说法正确的是( )
 如图所示,理想变压器输入交变电压u=220$\sqrt{2}$sin100πt(V),理想变压器原、副线圈匝数比为2:1,已知电水壶额定功率为880W,排气扇机内电阻为1Ω,电流表示数为18A,各用电器均正常工作.电流表为理想电表.下列说法正确的是( )
如图所示,理想变压器输入交变电压u=220$\sqrt{2}$sin100πt(V),理想变压器原、副线圈匝数比为2:1,已知电水壶额定功率为880W,排气扇机内电阻为1Ω,电流表示数为18A,各用电器均正常工作.电流表为理想电表.下列说法正确的是( )| A. | 变压器的输入功率为1980W | |
| B. | 通过排气扇的电流为15A | |
| C. | 排气扇的输出功率为1000W | |
| D. | 理想变压器输出电压表达式为u=110$\sqrt{2}$cos50π t(V) |
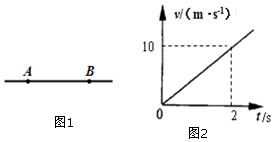 如图,A、B是-条电场线上的两点,t=0时刻从A点释放一初速为零的电子,电子仅在电场力作用下,沿直线从A运动到B,其速度随时间变化的规律如图所示.t=2s时到达B点速度大小为10m/s.已知电子质量为m,电荷量大小为e.求:
如图,A、B是-条电场线上的两点,t=0时刻从A点释放一初速为零的电子,电子仅在电场力作用下,沿直线从A运动到B,其速度随时间变化的规律如图所示.t=2s时到达B点速度大小为10m/s.已知电子质量为m,电荷量大小为e.求:

 如图所示,当S接通或断开时,线圈A、B中分别产生了什么方向的感应电流?为什么说各匝内的感应电动势是同方向的,总电动势是每一匝内的电动势之和?
如图所示,当S接通或断开时,线圈A、B中分别产生了什么方向的感应电流?为什么说各匝内的感应电动势是同方向的,总电动势是每一匝内的电动势之和?