题目内容
19．
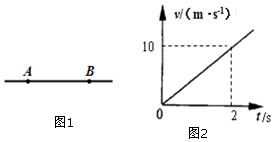如图，A、B是-条电场线上的两点，t=0时刻从A点释放一初速为零的电子，电子仅在电场力作用下，沿直线从A运动到B，其速度随时间变化的规律如图所示．t=2s时到达B点速度大小为10m/s．已知电子质量为m，电荷量大小为e．求：（1）电子运动的加速度大小为多少？
（2）A点的场强的大小和方向；
（3）AB间的电势差UAB．
分析 （1）由图象知电子做匀加速运动，由图象求得加速度
（2）根据电子的运动性质可明确电场为匀强电场，根据牛顿定律结合E=$\frac{F}{q}$求得电场强度
（3）由动能定理结合电场力做功与电势差的关系求得AB间的电势差
解答 解：（1）由图象知电子做匀加速运动，加速度为：a=$\frac{△v}{△t}$=$\frac{10}{2}$=5m/s2
（2）由eE=ma
得：E=$\frac{ma}{e}$=$\frac{5m}{e}$
电子带负电，电场力由A到B，故场强沿BA方向
（2）从A到B由动能定理有：-eUAB=$\frac{1}{2}$mv2
得：UAB=-$\frac{50m}{e}$
答：（1）加速度为5m/s2
（2）A点的场强的大小为$\frac{5m}{e}$，方向由B到A；
（2）AB间的电势差为-$\frac{50m}{e}$
点评 本题考查匀强电场的性质，解题的关键是从图象得到加速度，由电场强度定义式结合牛顿第二定律以及动能定理求解即可，注意在计算电功时要明确各物理量符号，并能准确代入计算．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，实线代表三根首尾相接的等长绝缘细棒，棒上的电荷分布情况与绝缘棒换成等长的细导体棒时的电荷分布完全相同．点A是△abc的中心，B点和A点相对bc边对称，已测得A、B两点的电势分别为UA和UB．现将绝缘棒ab取走，设这不影响ac、bc棒的电荷分布，试求此时A点的电势$\frac{2}{3}$UA，B点的电势$\frac{1}{6}$UA+$\frac{1}{2}$UB．
将比荷不同的离子分开，是原子核物理研究中的一项重要技术．一种方法是利用如图1所示的装置，在边界AC上方存在有区域足够大的方向垂直纸面向里的匀强磁场，磁感应强度为B，边界AC上有一狭缝．离子源放射出初速度可以忽略的正离子，离子进入电场并经电场加速后，穿过狭缝沿垂直于边界AC且垂直于磁场的方向射入磁场，最后打在置有离子接收器的区域CD上被收集．已知区域CD的右边界距狭缝的距离为L，左边界距狭缝足够远，整个装置内部为真空，不计离子重力，也不考虑离子间的相互作用．
7．
如图（a）所示，光滑绝缘水平面上有甲、乙两个点电荷，质量分别为m、M．t=0时，甲静止，乙以初速度6m/s向甲运动．此后，它们仅在静电力的作用下沿同一直线运动（整个运动过程中没有接触），它们运动的v-t图象分别如图（b）中甲、乙两曲线所示．则由图线可知（ ）
如图（a）所示，光滑绝缘水平面上有甲、乙两个点电荷，质量分别为m、M．t=0时，甲静止，乙以初速度6m/s向甲运动．此后，它们仅在静电力的作用下沿同一直线运动（整个运动过程中没有接触），它们运动的v-t图象分别如图（b）中甲、乙两曲线所示．则由图线可知（ ）| A． | m=2M | |
| B． | t1时刻两电荷的电势能最大 | |
| C． | 0～t2时间内，两电荷的静电力先增大后减小 | |
| D． | 运动过程中，甲的动能一直增大，乙的动能一直减小 |
14．下列说法正确的是（ ）
| A． | 随着分子间距离增大，分子斥力不断减小，分子引力不断增大 | |
| B． | 功转变为热的实际宏观过程是不可逆过程 | |
| C． | 荷叶上的小水珠呈球形是水的表面张力作用的结果 | |
| D． | 0℃的水和0℃的冰分子平均动能相同 | |
| E． | 彩色液晶显示器利用了液晶的光学性质具有各向同性的特点 |
4．
如图所示，劲度系数分别为K1和K2的两根弹簧，K1＞K2，质量m1，m2的两个小物块，且m1＞m2，现要求两根弹簧的总长最短，则应使（ ）
如图所示，劲度系数分别为K1和K2的两根弹簧，K1＞K2，质量m1，m2的两个小物块，且m1＞m2，现要求两根弹簧的总长最短，则应使（ ）| A． | K1在上，m1在上 | B． | K1在上，m2在上 | C． | K2在上，m1在上 | D． | K2在上，m2在上 |
如图所示，物体A、B叠放在倾角α=37°的斜面上，并通过细线跨过光滑滑轮相连，细线与斜面平行．两物体的质量分别为mA=5kg，mB=10kg，A、B间动摩擦因数为μ1=0.1，B与斜面间的动摩擦因数为μ2=0.2，现对A施一平行于斜面向下的拉力F，使A平行于斜面向下匀速运动（A，B始终接触），（g=10m/s2，sin37°=0.6，cos37°=0.8）．
如图所示，两根相距L=0.5m，电阻不计的平行光滑金属导轨MN、PQ水平放置，导轨的一段与组织R0=0.3Ω的电阻相连，在导轨MN、PQ所在平面内建立直角坐标系xOy，Ox轴沿PQ方向，垂直于导轨平面向里的非均强磁场的磁感应强度大小沿x轴方向的变化规律为B=（0.8+0.2x）T（其中x的单位是m），一根质量m=0.2kg、电阻r=0.1Ω的金属棒ab置于导轨上，并与导轨垂直，金属棒ab在外力作用下从x=0处以初速度v0=3m/s沿导轨水平向右运动，运动过程中电路总电阻消耗的功率不变，求：
如图所示，竖直放置的绝热圆柱形容器内用绝热活塞封闭一定质量的理想气体，已知容器横截面积为S，活塞重为G1，与容器底部相距h，大气压强为p0，现通过电热丝缓慢加热气体，当气体的温度为T1时活塞上升了$\frac{h}{2}$，此时停止对气体加热，同时在活塞上缓慢添加砂粒，当添加砂粒的重为G0时，活塞恰好回到原来位置，不计摩擦，求此时气体的温度．