题目内容
7.箩筐内盛有多只西瓜,放在倾角为θ的斜面上.给箩筐一个沿斜面向下的初速度v0,使箩筐与西瓜一起沿斜面滑行(在滑行过程中西瓜在筐内的相对位置保持不变),滑行一段距离后停下.设箩筐与斜面间的动摩擦因数为μ,则在滑行途中,筐内质量为m的某个西瓜(未与箩筐接触)受到周围西瓜的作用力大小为( )| A. | μmgcosθ+mgsinθ | B. | μmgcosθ-mgsinθ | C. | mg$\sqrt{1+{μ}^{2}}$cosθ | D. | mg$\sqrt{1-{μ}^{2}}$cosθ |
分析 对箩筐与西瓜整体为研究对象,求出整体加速度,再对某个西瓜为研究对象,受到重力,周围西瓜的作用力,运用正交分解法求出周围西瓜的作用力.
解答 解:对箩筐与西瓜组成的整体为研究对象,受力分析如图,
根据牛顿第二定律,有
μMgcosθ-Mgsinθ=Ma
解得:a=μgcosθ-gsinθ①
以某个西瓜为研究对象,进行受力分析,受到重力和周围西瓜的作用力,受力分析如图
根据牛顿第二定律,有
垂直斜面方向:${F}_{2}^{\;}=mgcosθ$②
平行斜面方向:${F}_{1}^{\;}-mgsinθ=ma$③
解得:${F}_{1}^{\;}=μmgcosθ$
周围西瓜对某个西瓜的作用力:$F=\sqrt{{F}_{1}^{2}+{F}_{2}^{2}}=\sqrt{(μmgcosθ)_{\;}^{2}+(mgcosθ)_{\;}^{2}}$=$\sqrt{1+{μ}_{\;}^{2}}mgcosθ$,故C正确,ABD错误;
故选:C
点评 解决本题的关键抓住加速度相同,结合牛顿第二定律进行求解

练习册系列答案
相关题目
15. 如图所示,原本不带电的金属球A的半径为R,球外放一个带电荷量为Q、到球心O的距离为r的点电荷.则当金属球达到静电平衡时感应电荷在球心O处产生的场强大小等于( )
如图所示,原本不带电的金属球A的半径为R,球外放一个带电荷量为Q、到球心O的距离为r的点电荷.则当金属球达到静电平衡时感应电荷在球心O处产生的场强大小等于( )
 如图所示,原本不带电的金属球A的半径为R,球外放一个带电荷量为Q、到球心O的距离为r的点电荷.则当金属球达到静电平衡时感应电荷在球心O处产生的场强大小等于( )
如图所示,原本不带电的金属球A的半径为R,球外放一个带电荷量为Q、到球心O的距离为r的点电荷.则当金属球达到静电平衡时感应电荷在球心O处产生的场强大小等于( )| A. | k$\frac{Q}{{r}^{2}}$-k$\frac{Q}{{R}^{2}}$ | B. | k$\frac{Q}{{r}^{2}}$+k$\frac{Q}{{R}^{2}}$ | C. | 0 | D. | k$\frac{Q}{{r}^{2}}$ |
18. 如图所示,a、b、c、d、e、f点是以O为球心的球面上的点,分别在a、c两点处放上等量异种电荷+Q和-Q.下列说法正确的是( )
如图所示,a、b、c、d、e、f点是以O为球心的球面上的点,分别在a、c两点处放上等量异种电荷+Q和-Q.下列说法正确的是( )
 如图所示,a、b、c、d、e、f点是以O为球心的球面上的点,分别在a、c两点处放上等量异种电荷+Q和-Q.下列说法正确的是( )
如图所示,a、b、c、d、e、f点是以O为球心的球面上的点,分别在a、c两点处放上等量异种电荷+Q和-Q.下列说法正确的是( )| A. | b、f两点电场强度大小相等,方向不同 | |
| B. | e、d两点电势不同 | |
| C. | b、f两点电场强度大小相等,方向相同 | |
| D. | e、d两点电势相同 |
12.一根轻绳跨过一轻定滑轮,质量为m的人抓着绳的一端,另一端系了一个质量为$\frac{m}{2}$的物体,若人相对于绳匀速上爬时,物体上升的加速度为( )
| A. | $\frac{3}{2}g$ | B. | $\frac{1}{3}g$ | C. | $\frac{1}{2}g$ | D. | 2g |
19. 如图所示,在半径为R的圆形区域内存在方向垂直纸面向里的匀强磁场,O为圆心,ab为直径,c为圆上一点,∠aOc=60°.甲、乙两带电粒子以相同的速率分别从a、b两端点沿半径方向射向O点,两粒子都能从c点离开磁场,不计粒子重力,则( )
如图所示,在半径为R的圆形区域内存在方向垂直纸面向里的匀强磁场,O为圆心,ab为直径,c为圆上一点,∠aOc=60°.甲、乙两带电粒子以相同的速率分别从a、b两端点沿半径方向射向O点,两粒子都能从c点离开磁场,不计粒子重力,则( )
 如图所示,在半径为R的圆形区域内存在方向垂直纸面向里的匀强磁场,O为圆心,ab为直径,c为圆上一点,∠aOc=60°.甲、乙两带电粒子以相同的速率分别从a、b两端点沿半径方向射向O点,两粒子都能从c点离开磁场,不计粒子重力,则( )
如图所示,在半径为R的圆形区域内存在方向垂直纸面向里的匀强磁场,O为圆心,ab为直径,c为圆上一点,∠aOc=60°.甲、乙两带电粒子以相同的速率分别从a、b两端点沿半径方向射向O点,两粒子都能从c点离开磁场,不计粒子重力,则( )| A. | 甲粒子带正电、乙粒子带负电 | |
| B. | 甲、乙两粒子的比荷之比为3:1 | |
| C. | 甲、乙两粒子的比荷之比为2:1 | |
| D. | 甲、乙两粒子离开磁场时的速度方向不同 |
16. 在平行于纸面的匀强电场中,电子由A点以初速度v0向各个方向飞出,有两个电子能以相同大小的速度v1分别经过B、C两点,v0>v1,电子间相互作用力和重力不计,下列说法中正确的是( )
在平行于纸面的匀强电场中,电子由A点以初速度v0向各个方向飞出,有两个电子能以相同大小的速度v1分别经过B、C两点,v0>v1,电子间相互作用力和重力不计,下列说法中正确的是( )
 在平行于纸面的匀强电场中,电子由A点以初速度v0向各个方向飞出,有两个电子能以相同大小的速度v1分别经过B、C两点,v0>v1,电子间相互作用力和重力不计,下列说法中正确的是( )
在平行于纸面的匀强电场中,电子由A点以初速度v0向各个方向飞出,有两个电子能以相同大小的速度v1分别经过B、C两点,v0>v1,电子间相互作用力和重力不计,下列说法中正确的是( )| A. | A点电势高于C点电势 | B. | A点电势低于B点电势 | ||
| C. | 电场强度方向平行于BC | D. | 电场强度方向垂直于BC |
 如图所示,abcd是一个边长为L的正方形盒子,cd边水平,其中点有一个小孔e,盒子中有沿ad方向(竖直向下)匀强电场.一质量为m、电荷量为q的带正电小球从a处的水上孔沿ab方向以初速度v0射入盒内,并恰好从小孔e处射出.重力加速度为g.求:
如图所示,abcd是一个边长为L的正方形盒子,cd边水平,其中点有一个小孔e,盒子中有沿ad方向(竖直向下)匀强电场.一质量为m、电荷量为q的带正电小球从a处的水上孔沿ab方向以初速度v0射入盒内,并恰好从小孔e处射出.重力加速度为g.求:
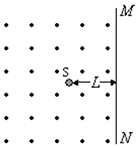 如图所示,粒子源S能在图示纸面内的360°范围内发射速率相同、质量为m、电量为+q的同种粒子(重力不计),MN是足够大的竖直挡板,S到板的距离为L,挡板左侧充满垂直纸面向外的匀强磁场,磁感应强度为B,求:
如图所示,粒子源S能在图示纸面内的360°范围内发射速率相同、质量为m、电量为+q的同种粒子(重力不计),MN是足够大的竖直挡板,S到板的距离为L,挡板左侧充满垂直纸面向外的匀强磁场,磁感应强度为B,求: