题目内容
2.如图1所示,平行板电容器的M、N两板间距为d,两板间存在竖直向上的匀强电场E,M、N的正中央各有一小孔.在上板小孔正上方有一竖直放置长为l的轻质绝缘细杆,细杆的上下两端分别固定一个带点小球A、B,它们的质量均为m=0.01kg,A带q1=2.5×10-4C的正电,B带q2=5×10-5C的负电,B球距上板M的距离为h,现将轻杆由静止释放,小球B从刚进入电场到刚好离开电场过程中的v-t图象如图2所示(忽略空气阻力,g=10m/s2).(1)试求匀强电场E及板间距离d;
(2)试判定A球能否从下板离开匀强电场.

分析 (1)将轻杆由静止释放后AB两个小球先做自由落体运动,B进入电场后受到电场力作用,由图2求出加速度,对AB球整体进行受力分析,结合牛顿第二定律写出动力学方程;然后A球进入电场,由图求出加速度,再进行受力分析,写出动力学方程,即可求出;
(2)最后B离开电场时,A还在电场中,再次对AB整体进行受力分析,求出加速度,分析运动情况,即可判定A球能否从下板离开匀强电场.
解答 解:(1)将轻杆由静止释放到B刚好进入磁场的过程中,AB两个小球做自由落体运动,在B进入电场而A没有进入电场的过程中由图可知它们的加速度:
${a}_{1}=\frac{△v}{△t}=\frac{4-1}{0.3-0.1}=15$m/s2
对AB球整体进行受力分析得:2mg+q1E=2ma1
代入数据得:E=2000N/C
B进入电场时的速度:v0=1m/s,最大速度是4m/s,出电场时的速度是2m/s,由匀变速直线运动的v-t图象的特点可得:
d=$\frac{1+4}{2}×(0.3-0.1)+\frac{4+2}{2}×(0.5-0.3)$=1.1m
(2)由图2可知,轻质绝缘细杆的长度:
l=$\frac{1+4}{2}×(0.3-0.1)=0.5$m
B出电场时,A到电场的下边的距离:x=d-l=1.1-0.5=0.6m
B出电场后A、B系统的加速度大小:${a}_{2}=\frac{2mg-{q}_{2}E}{2m}$
代入数据得:${a}_{2}=-15m/{s}^{2}$
若A不离开N板,当A速度减小到0时A下降的高度为s,由运动学公式有:0-v2=2a2s
则:s=$\frac{-{v}^{2}}{2{a}_{2}}=\frac{-{2}^{2}}{2×(-15)}=\frac{2}{15}$m<0.6m
故A球不能从下板离开匀强电场,以后反向加速运动.
答:(1)匀强电场s 200N/C,板间距离是1.1m;
(2)不能离开,当A速度减小到0时,还在电场中,以后反向加速运动.
点评 本题解题的关键是对AB两小球进行受力分析,根据受力情况分析运动情况,结合运动学基本公式及牛顿第二定律求解,难度适中.

 一带负电的粒子只在电场力作用下沿x轴正方向运动,其电势能 Ep随位移x变化的关系如图所示,其中0-x2段是关于直线x=x1对称的曲线,x2-x3段是直线,则下列说法正确的是( )
一带负电的粒子只在电场力作用下沿x轴正方向运动,其电势能 Ep随位移x变化的关系如图所示,其中0-x2段是关于直线x=x1对称的曲线,x2-x3段是直线,则下列说法正确的是( )| A. | x1处电场强度为零 | |
| B. | 粒子在0-x2段做匀变速运动,x2-x3段做匀速直线运动 | |
| C. | 在0、x1、x2、x3处电势 φ0、φ1、φ2、φ3的关系为 φ3>φ2=φ0>φ1 | |
| D. | x2-x3段的电场强度大小方向均不变 |
 如图所示,从炽热的金属丝飘出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )
如图所示,从炽热的金属丝飘出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )| A. | 仅将偏转电场极性对调一下位置 | |
| B. | 增大偏转电极板间的电压,减小两板间的距离 | |
| C. | 增大偏转电极板间的距离,减小偏转电极的电压 | |
| D. | 减小偏转电极板间的电压,增大加速电压 |
| A. | μmgcosθ+mgsinθ | B. | μmgcosθ-mgsinθ | C. | mg$\sqrt{1+{μ}^{2}}$cosθ | D. | mg$\sqrt{1-{μ}^{2}}$cosθ |
 如图所示,左侧为两块长为L=10cm,间距d=$\frac{10\sqrt{3}}{3}$cm的平行金属板,加U=$\frac{10}{3}$×104V的电压,上板电势低,用虚线框表示的等边三角形内存在垂直纸面向里的匀强磁场B,三角形的上顶点A与上金属板平齐,DC边与金属板平行,AD的中点P恰好在下金属板的右端点.现从AC边的中点Q以初速度v=$\frac{2\sqrt{3}}{3}$×105m/s垂直AC边射入一个重力不计的带负电微粒,微粒质量m=10-10kg,带电量q=-10-4C,若要使粒子刚好从P点垂直AD边射出磁场进入极板,求:
如图所示,左侧为两块长为L=10cm,间距d=$\frac{10\sqrt{3}}{3}$cm的平行金属板,加U=$\frac{10}{3}$×104V的电压,上板电势低,用虚线框表示的等边三角形内存在垂直纸面向里的匀强磁场B,三角形的上顶点A与上金属板平齐,DC边与金属板平行,AD的中点P恰好在下金属板的右端点.现从AC边的中点Q以初速度v=$\frac{2\sqrt{3}}{3}$×105m/s垂直AC边射入一个重力不计的带负电微粒,微粒质量m=10-10kg,带电量q=-10-4C,若要使粒子刚好从P点垂直AD边射出磁场进入极板,求: 如图所示:绝缘中空轨道竖直固定,圆弧段COD光滑,对应圆心角为120°,C、D两端等高,O为最低点,圆弧圆心为O′,半径为R;直线段AC、HD粗糙,与圆弧段分别在C、D端相切;整个装置处于方向垂直于轨道所在平面向里、磁感应强度为B的匀强磁场中,在竖直虚线MC左侧和ND右侧还分别存在着场强大小相等、方向水平向右和向左的匀强电场.现有一质量为m、电荷量恒为q、直径略小于轨道内径、可视为质点的带正电小球,从轨道内距C点足够远的P点由静止释放.已知PC=L,小球所受重力大小为电场力的$\sqrt{3}$倍,重力加速度为g.
如图所示:绝缘中空轨道竖直固定,圆弧段COD光滑,对应圆心角为120°,C、D两端等高,O为最低点,圆弧圆心为O′,半径为R;直线段AC、HD粗糙,与圆弧段分别在C、D端相切;整个装置处于方向垂直于轨道所在平面向里、磁感应强度为B的匀强磁场中,在竖直虚线MC左侧和ND右侧还分别存在着场强大小相等、方向水平向右和向左的匀强电场.现有一质量为m、电荷量恒为q、直径略小于轨道内径、可视为质点的带正电小球,从轨道内距C点足够远的P点由静止释放.已知PC=L,小球所受重力大小为电场力的$\sqrt{3}$倍,重力加速度为g. 如图所示,足够长的绝缘斜面与水平面的夹角为37°(sin37°=0.6),放在水平方向的匀强电场和匀强磁场中,电场强度E=50v/m方向水平向左,磁场方向垂直纸面向里.一个电量为q=-4.0×10-2C,质量为m=0.4kg的光滑小球以初速度v0=20m/s从斜面底端向上滑,然后又滑下,共经过3s脱离斜面,求磁场的磁感应强度多大?(g=10m/s2)
如图所示,足够长的绝缘斜面与水平面的夹角为37°(sin37°=0.6),放在水平方向的匀强电场和匀强磁场中,电场强度E=50v/m方向水平向左,磁场方向垂直纸面向里.一个电量为q=-4.0×10-2C,质量为m=0.4kg的光滑小球以初速度v0=20m/s从斜面底端向上滑,然后又滑下,共经过3s脱离斜面,求磁场的磁感应强度多大?(g=10m/s2) 如图所示,在边长为L的等边三角形内有垂直纸面向里的匀强磁场,磁感应强度为B,D是底边AB的中点,质量为m,电荷量为q的带正电的粒子(不计重力)可以从AB边上不同的位置以不同的速度竖直向上射入磁场.
如图所示,在边长为L的等边三角形内有垂直纸面向里的匀强磁场,磁感应强度为B,D是底边AB的中点,质量为m,电荷量为q的带正电的粒子(不计重力)可以从AB边上不同的位置以不同的速度竖直向上射入磁场.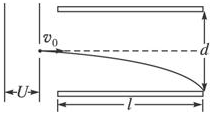 一带电荷量q=4.0×10-8C质量为m=1.0×10-14粒子在经U=5000V的加速电压加速后,在距两极板间中央处垂直进入平行板间的匀强电场,如图所示,若两板间距d=1.0m,板长L=5.0m,那么,(重力不计)
一带电荷量q=4.0×10-8C质量为m=1.0×10-14粒子在经U=5000V的加速电压加速后,在距两极板间中央处垂直进入平行板间的匀强电场,如图所示,若两板间距d=1.0m,板长L=5.0m,那么,(重力不计)