题目内容
15. 如图所示,abcd是一个边长为L的正方形盒子,cd边水平,其中点有一个小孔e,盒子中有沿ad方向(竖直向下)匀强电场.一质量为m、电荷量为q的带正电小球从a处的水上孔沿ab方向以初速度v0射入盒内,并恰好从小孔e处射出.重力加速度为g.求:
如图所示,abcd是一个边长为L的正方形盒子,cd边水平,其中点有一个小孔e,盒子中有沿ad方向(竖直向下)匀强电场.一质量为m、电荷量为q的带正电小球从a处的水上孔沿ab方向以初速度v0射入盒内,并恰好从小孔e处射出.重力加速度为g.求:(1)该小球从e孔射出的速度大小v;
(2)该电场的电场强度大小E.
分析 (1)粒子进入电场后水平方向做匀速直线运动,竖直方向做匀加速直线运动,用平均速度表示竖直位移和水平位移,求出粒子从e孔射出时竖直方向的速度,再合成求解粒子从e孔射出的速度大小.
(2)根据牛顿第二定律和位移公式结合求出电场强度.
解答  解:(1)如图,设正方形边长为L,离开电场时竖直方向速度vy
解:(1)如图,设正方形边长为L,离开电场时竖直方向速度vy
(1)a→e 粒子做类平抛运动
沿v0方向:$\frac{L}{2}={v_0}t$
沿E方向:$L=\frac{v_y}{2}t$
解得:vy=4v0
离开电场时速度大小$v=\sqrt{v_0^2+v_y^2}=\sqrt{17}{v_0}$
(2)根据牛顿第二定律得,加速度a=$\frac{qE}{m}$,y=l=$\frac{1}{2}a{t}^{2}$,t=$\frac{1}{2}•$$\frac{l}{{v}_{0}}$
联立得,E=$\frac{8m{v}_{0}^{2}}{ql}$
答:(1)该带电粒子从e孔射出时的速度大小是$\sqrt{17}{v}_{0}$.
(2)该电场的电场强度大小E是$\frac{8m{v}_{0}^{2}}{ql}$.
点评 本题是类平抛运动问题,基本方法是运动的分解法,要抓住水平和竖直两个方向位移的关系是关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
3. 如图所示,博尔特在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩破两项世界纪录,获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )
如图所示,博尔特在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩破两项世界纪录,获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )
 如图所示,博尔特在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩破两项世界纪录,获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )
如图所示,博尔特在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩破两项世界纪录,获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )| A. | 200 m决赛中的位移是100 m决赛的两倍 | |
| B. | 200 m决赛中的路程是100 m决赛的两倍 | |
| C. | 200 m决赛中的平均速度大小约为10.36 m/s | |
| D. | 100 m决赛中的平均速度大小约为10.32 m/s |
3. 如图所示,在两条竖直边界线所围的匀强电场中,一个不计重力的带电粒子从左边界的P点以某一水平速度射入电场,从右边界的Q点射出,下列判断正确的有( )
如图所示,在两条竖直边界线所围的匀强电场中,一个不计重力的带电粒子从左边界的P点以某一水平速度射入电场,从右边界的Q点射出,下列判断正确的有( )
 如图所示,在两条竖直边界线所围的匀强电场中,一个不计重力的带电粒子从左边界的P点以某一水平速度射入电场,从右边界的Q点射出,下列判断正确的有( )
如图所示,在两条竖直边界线所围的匀强电场中,一个不计重力的带电粒子从左边界的P点以某一水平速度射入电场,从右边界的Q点射出,下列判断正确的有( )| A. | 粒子带负电 | |
| B. | 粒子做匀速圆周运动 | |
| C. | 粒子电势能增大 | |
| D. | 仅增大电场强度粒子通过电场的时间不变 |
10. 如图所示,从炽热的金属丝飘出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )
如图所示,从炽热的金属丝飘出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )
 如图所示,从炽热的金属丝飘出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )
如图所示,从炽热的金属丝飘出的电子(速度可视为零),经加速电场加速后从两极板中间垂直射入偏转电场.电子的重力不计.在满足电子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的是( )| A. | 仅将偏转电场极性对调一下位置 | |
| B. | 增大偏转电极板间的电压,减小两板间的距离 | |
| C. | 增大偏转电极板间的距离,减小偏转电极的电压 | |
| D. | 减小偏转电极板间的电压,增大加速电压 |
20. 如图所示,悬线下悬挂着一个带正电的小球,它的质量为m,电量为q,整个装置处于水平向右的匀强电场中,电场强度为E,小球静止,则下列说法正确的是( )
如图所示,悬线下悬挂着一个带正电的小球,它的质量为m,电量为q,整个装置处于水平向右的匀强电场中,电场强度为E,小球静止,则下列说法正确的是( )
 如图所示,悬线下悬挂着一个带正电的小球,它的质量为m,电量为q,整个装置处于水平向右的匀强电场中,电场强度为E,小球静止,则下列说法正确的是( )
如图所示,悬线下悬挂着一个带正电的小球,它的质量为m,电量为q,整个装置处于水平向右的匀强电场中,电场强度为E,小球静止,则下列说法正确的是( )| A. | 若剪断悬线,小球做圆周运动 | |
| B. | 若剪断悬线,小球做曲线运动 | |
| C. | 若剪断悬线,小球做匀速运动 | |
| D. | 若剪断悬线,小球做匀加速直线运动 |
7.箩筐内盛有多只西瓜,放在倾角为θ的斜面上.给箩筐一个沿斜面向下的初速度v0,使箩筐与西瓜一起沿斜面滑行(在滑行过程中西瓜在筐内的相对位置保持不变),滑行一段距离后停下.设箩筐与斜面间的动摩擦因数为μ,则在滑行途中,筐内质量为m的某个西瓜(未与箩筐接触)受到周围西瓜的作用力大小为( )
| A. | μmgcosθ+mgsinθ | B. | μmgcosθ-mgsinθ | C. | mg$\sqrt{1+{μ}^{2}}$cosθ | D. | mg$\sqrt{1-{μ}^{2}}$cosθ |
5.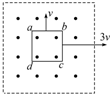 如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )
如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )
 如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )
如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面的、电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中( )| A. | 导体框中产生的感应电流方向相同 | B. | 导体框中产生的焦耳热相同 | ||
| C. | 导体框ad边两端电势差相同 | D. | 通过导体框截面的电荷量相同 |
 如图甲所示,两根平行光滑金属导轨相距L=1m,导轨平面与水平面的夹角θ=30°,导轨的下端PQ间接有R=8Ω电阻.相距x=6m的MN和PQ间存在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场.磁感应强度B随时间t的变化情况如图乙所示.将阻值r=2Ω的导体棒ab垂直放在导轨上,使导体棒从t=0时由静止释放,t=1s时导体棒恰好运动到MN,开始匀速下滑.g取10m/s2.求:
如图甲所示,两根平行光滑金属导轨相距L=1m,导轨平面与水平面的夹角θ=30°,导轨的下端PQ间接有R=8Ω电阻.相距x=6m的MN和PQ间存在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场.磁感应强度B随时间t的变化情况如图乙所示.将阻值r=2Ω的导体棒ab垂直放在导轨上,使导体棒从t=0时由静止释放,t=1s时导体棒恰好运动到MN,开始匀速下滑.g取10m/s2.求: 如图所示,静止放在水平光滑的桌面上的纸带,其上有一质量为m=0.5kg的铁块,它与纸带右端的距离为L=0.5m,铁块与纸带间的动摩擦因数为μ=0.1.现用力F水平向左将纸带从铁块下抽出,当纸带全部抽出时铁块恰好到达桌面边缘,铁块抛出后落地点离抛出点的水平距离为s=0.8m.已知g=10m/s2,桌面高度为H=0.8m,不计纸带质量,不计铁块大小,铁块不翻滚.求:
如图所示,静止放在水平光滑的桌面上的纸带,其上有一质量为m=0.5kg的铁块,它与纸带右端的距离为L=0.5m,铁块与纸带间的动摩擦因数为μ=0.1.现用力F水平向左将纸带从铁块下抽出,当纸带全部抽出时铁块恰好到达桌面边缘,铁块抛出后落地点离抛出点的水平距离为s=0.8m.已知g=10m/s2,桌面高度为H=0.8m,不计纸带质量,不计铁块大小,铁块不翻滚.求: