题目内容
18. 如图所示为甲乙两物体的一次运动的速度-时间图象:
如图所示为甲乙两物体的一次运动的速度-时间图象:(1)求前1秒内甲乙两物体的加速度;
(2)求后2秒内甲乙两物体的加速度;
(3)通过上述计算,你可以发现加速度与速度-时间图象有什么关系吗?
分析 首先知道速度时间图象的意义,据斜率表示 加速度求解;注意加速度单位和甲乙两物体的运动情况.
解答 解:(1)据图象的意义可知,甲沿正方向做初速度为零的匀加速直线运动;据速度时间图象的斜率表示加速度,a甲=$\frac{60}{4}km/{h}^{2}$=15Km/h2
乙在前1秒内物体的加速度:a乙=$\frac{-30}{1}Km/{h}^{2}$=-30Km/h2
(2)由于甲做匀加速直线运动,所以甲的加速度不变,即为,a甲=$\frac{60}{4}km/{h}^{2}$=15Km/h2
乙在后2秒内物体的加速度:a乙=$\frac{60-(-30)}{4-2}Km/{h}^{2}$=45Km/h2
(3)以上可知,加速度与速度没有直接的关系,取决于单位时间内速度的变化,即速度时间图象的斜率表示加速度.
答:(1)求前1秒内甲乙两物体的加速度分别为15Km/h2和-30Km/h2;
(2)求后2秒内甲乙两物体的加速度15Km/h2和45Km/h2;
(3)通过上述计算可知,加速度与速度没有直接的关系,取决于单位时间内速度的变化,即速度时间图象的斜率表示加速度
点评 知道速度时间图象的意义,利用图象的斜率求解加速度;注意加速度单位否则计算难度较大,常规题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
8.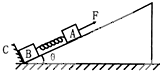 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )| A. | 拉力F做功的等于A动能的增加量 | |
| B. | 物块B满足m2gsinθ=kd | |
| C. | 物块A的加速度为$\frac{F-kd}{{m}_{1}}$ | |
| D. | 弹簧弹性势能的增加量为Fd-m1gdsinθ-$\frac{1}{2}$m1v2 |
9. 真空中三维坐标系Oxyz的z轴方向竖直向上,在坐标原点0上固定一带正电的点电荷Q,其形成的电场如图所示,一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动.则( )
真空中三维坐标系Oxyz的z轴方向竖直向上,在坐标原点0上固定一带正电的点电荷Q,其形成的电场如图所示,一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动.则( )
 真空中三维坐标系Oxyz的z轴方向竖直向上,在坐标原点0上固定一带正电的点电荷Q,其形成的电场如图所示,一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动.则( )
真空中三维坐标系Oxyz的z轴方向竖直向上,在坐标原点0上固定一带正电的点电荷Q,其形成的电场如图所示,一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动.则( )| A. | 该微粒带负电,轨道圆心在坐标原点O上 | |
| B. | 该微粒带负电,轨道圆心在z轴的负半轴上某一点 | |
| C. | 该微粒带正电,轨道圆心在坐标原点0上 | |
| D. | 该微粒带正电,轨道圆心在z轴的正半轴上某一点 |
3.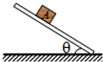 如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )
如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )
 如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )
如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )| A. | 物块与木板之间的摩擦因数μ=$\frac{\sqrt{3}}{3}$ | |
| B. | 将木块与水平面的视角改为60°,再释放物块,其运动加速度为$\frac{10\sqrt{3}}{3}$m/s2 | |
| C. | 将木板与水平面的倾角改为60°,再释放物块,其运动到木板下端的速度为2$\sqrt{3}$m/s | |
| D. | 将木板与水平桌面的倾角改为60°,再释放物块,其运动到木板下端的过程中重力做功5$\sqrt{3}$J |
8.天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,已知两颗恒星之间的距离、周期、其中一颗星的质量和万有引力常量,可得出( )
| A. | 另一颗星的质量 | |
| B. | 每颗星的线速度与自身的轨道半径成反比 | |
| C. | 每颗星的质量与自身的孰道半径成正比 | |
| D. | 每颗星的质量与自身的轨道半径成反比 |

