��Ŀ����
17����ͼ��ʾ����ֱ������ϵxOy����a��b��c��d�ĵ㣬��֪oa=L��ob=od=2L��oc=2$\sqrt{2}$L���ڵ�һ�����У��߽�OM��x��֮���г�ǿΪE2����ǿ�ų�������ͱ߽�OMƽ�У��߽�OM��y��֮���дŸ�Ӧǿ��ΪB����ǿ�ų��������ֽ�洹ֱ���߽�OM��x��֮��ļнǦ�=45�㣩���ڶ������У��з�����x���������ǿ�ų�E1������һ�����Ϊ+q������Ϊm�Ĵ������ӣ���������������a����v0�ij��ٶȣ�������y����������糡����b�����ų�ƫת����c�㴹ֱOM����糡E2�����d�㣬��E1��E2��B��Ϊδ֪��������1��������b����ٶȴ�С��
��2����ǿ�ų�B�Ĵ�С�ͷ���
��3���糡ǿ��E2�Ĵ�С��
��4�����Ӵ�a�˶���d��ʱ�䣮

���� ��1�������ڵڶ�����������ƽ���˶��������˶�ѧ��ʽ��ץס��ʱ�����������b����x�᷽���ϵķ��ٶȣ����ƽ���ı��ζ������b����ٶȣ�
��2�����������ڴų����˶��Ĺ켣�����ݼ��ι�ϵ���������Բ���˶��İ뾶����ϰ뾶��ʽ����Ÿ�Ӧǿ�ȵĴ�С��ͨ�����ֶ����жϳ��ų��ķ���
��3�������ڵ糡E2������ƽ���˶��������ƽ���˶����ص糡�����ϵ�λ�ƺʹ�ֱ�糡�����ϵ�λ�ƣ�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ����糡ǿ��E2�Ĵ�С��
��4���ֶ����ʱ�䣬�õ���ʱ�䣮
��� �⣺��1�������ڵڶ����ĵ糡������ƽ���˶���
��v0t=2L��$\frac{{v}_{bx}}{2}$t=L��
������ʽ��� vbx=v0
����b����ٶȴ�С vb=$\sqrt{{v}_{0}^{2}+{v}_{x}^{2}}$=$\sqrt{2}$v0��
��2������b����ٶȵĴ��ߣ���bc�Ĵ�ֱƽ���ߣ�ȷ��Բ����ͼ����֪���Ӵ�ֱ����糡E2���ɼ��ι�ϵ�ɵ�Բ����İ뾶 r=$\sqrt{2}$L
���� qvbB=m$\frac{{v}_{b}^{2}}{r}$����� B=$\frac{m{v}_{0}}{qL}$������ֱֽ�����⣮
��3��������c�����糡E2������ƽ���˶���������ʱ��Ϊt2�����ٶ�Ϊa2�������˶����ɺ�ţ�ٵڶ������У�
$\sqrt{2}$L=$\sqrt{2}$v0t2��$\sqrt{2}$L=$\frac{1}{2}$a2t22��a2=$\frac{q{E}_{2}}{m}$
��� E2=$\frac{2\sqrt{2}m{v}_{0}^{2}}{qL}$��
��4����a��b���˶�ʱ�� t=$\frac{2L}{{v}_{0}}$
��b��c��ʱ�� t��=$\frac{1}{4}T$=$\frac{1}{4}•\frac{2��r}{{v}_{b}}$=$\frac{��L}{{2v}_{0}}$
�ɵ�3��֪��t2=$\frac{L}{{v}_{0}}$
�����Ӵ�a�˶���d��ʱ�� t��=t+t��+t2=$\frac{��6+�У�L}{2{v}_{0}}$
��
��1��������b����ٶȴ�СΪ $\sqrt{2}$v0��
��2����ǿ�ų�B�Ĵ�СΪ $\frac{m{v}_{0}}{qL}$������ֱֽ�����⣻
��3���糡ǿ��E2�Ĵ�СΪ$\frac{2\sqrt{2}m{v}_{0}^{2}}{qL}$��
��4�����Ӵ�a�˶���d��ʱ��Ϊ$\frac{��6+�У�L}{2{v}_{0}}$��
���� ��������ƽ��ʱ����ţ�ٵڶ��������˶�ѧ��ʽ�������ۺ����ã���������Բ���˶�ʱ���ɰ뾶��ʽ�뼸�ι�ϵ������Ӧ�ã��Ӷ�����ѧ���ڵ�ѧ����ѧ�ۺϽ����������

 ����5��2���ϵ�д�
����5��2���ϵ�д� ��ͼ��ʾ�����ɱ�����Ϊm��С��ѹ����С���뵯�ɲ�ճ���������ĸ߶�Ϊh����ֹʱϸ������ֱǽ�ļн�Ϊ�ȣ����ƿ����������ֽ���סС���ϸ���նϣ������С���Ժ��˵����ȷ���ǣ�������
��ͼ��ʾ�����ɱ�����Ϊm��С��ѹ����С���뵯�ɲ�ճ���������ĸ߶�Ϊh����ֹʱϸ������ֱǽ�ļн�Ϊ�ȣ����ƿ����������ֽ���סС���ϸ���նϣ������С���Ժ��˵����ȷ���ǣ�������| A�� | ֱ���˶� | B�� | �����˶� | ||
| C�� | �����ն�˲��ļ��ٶ�Ϊ0 | D�� | ���ʱ�Ķ��ܵ���mgh |
| A�� | ���ǵ����ٶ�֮��Ϊv1��v2=$\sqrt{2}$��1 | |
| B�� | ���ǵ��˶�����֮��ΪT1��T2=1��$2\sqrt{2}$ | |
| C�� | ���ǵ����ļ��ٶ�֮��Ϊa1��a2=4��1 | |
| D�� | ���ǵ�������֮��ΪF1��F2=4��1 |
 ����ͼ��ʾ�ľ���ʵ���·�У���֪�������ĵ���C1=C2=C����Դ�ĵ綯��ΪE������Ϊr�����ر�������Ϊ10k��������·�ﵽ�ȶ�״̬��������
����ͼ��ʾ�ľ���ʵ���·�У���֪�������ĵ���C1=C2=C����Դ�ĵ綯��ΪE������Ϊr�����ر�������Ϊ10k��������·�ﵽ�ȶ�״̬��������| A�� | ������ϵ��Ʋ�Ϊ�� | B�� | ���ؼ��ϵ��Ʋ�Ϊ�� | ||
| C�� | ������C1��������ΪCE | D�� | ������C2��������ΪCE |
 ��������һЩ���������ǽ�Զ������ϵͳ��������һ������ϵͳ��ͼ��ʾ������������ȵ�����λ�ڵȱ������ε����������ϣ�������������ľ����ΪR������������O������Բ���˶�������������������ǵ��������ã���������ΪG�����¶Ը�����ϵͳ��˵������ȷ���ǣ�������
��������һЩ���������ǽ�Զ������ϵͳ��������һ������ϵͳ��ͼ��ʾ������������ȵ�����λ�ڵȱ������ε����������ϣ�������������ľ����ΪR������������O������Բ���˶�������������������ǵ��������ã���������ΪG�����¶Ը�����ϵͳ��˵������ȷ���ǣ�������| A�� | ÿ��������Բ���˶��İ뾶������R | |
| B�� | ÿ��������Բ���˶��ļ��ٶ������������������ | |
| C�� | ÿ��������Բ���˶�������ΪT=2��R$\sqrt{\frac{R}{3Gm}}$ | |
| D�� | ÿ��������Բ���˶������ٶ�v=$\sqrt{\frac{Gm}{R}}$ |
 ��ͼ��ʾ����ֱ��ֽ���������ǿ�ų��ĴŸ�Ӧǿ��B=0.50T��MN�Ǵų�����߽磮�ڴų��е�A����һ��ֹ�غˣ�${\;}_{88}^{226}$Ra����A��MN�ľ���OA=1.00m��DΪ������MN��Ե�����ӽ�������OD=1.00m��${\;}_{88}^{226}$Ra����������˥�䣬�ų�ij������x���Ϊһ뱺ˣ�${\;}_{88}^{222}$Rn����������D���յ����ش�ֱ��MN��������������x��
��ͼ��ʾ����ֱ��ֽ���������ǿ�ų��ĴŸ�Ӧǿ��B=0.50T��MN�Ǵų�����߽磮�ڴų��е�A����һ��ֹ�غˣ�${\;}_{88}^{226}$Ra����A��MN�ľ���OA=1.00m��DΪ������MN��Ե�����ӽ�������OD=1.00m��${\;}_{88}^{226}$Ra����������˥�䣬�ų�ij������x���Ϊһ뱺ˣ�${\;}_{88}^{222}$Rn����������D���յ����ش�ֱ��MN��������������x��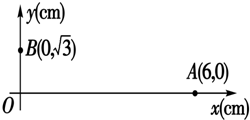 ��ͼ��ʾ����ƽ��ֱ������ϵ�У��з���ƽ��������ƽ�����ǿ�糡����������ԭ��O���ĵ���Ϊ0V����A���ĵ���Ϊ6V����B���ĵ���Ϊ3V����
��ͼ��ʾ����ƽ��ֱ������ϵ�У��з���ƽ��������ƽ�����ǿ�糡����������ԭ��O���ĵ���Ϊ0V����A���ĵ���Ϊ6V����B���ĵ���Ϊ3V����