题目内容
5. 如图所示为在水平面内做匀速圆周运动的圆锥摆.悬挂摆球的细线长度保持不变,关于摆球的受力和运动,下列说法正确的是( )
如图所示为在水平面内做匀速圆周运动的圆锥摆.悬挂摆球的细线长度保持不变,关于摆球的受力和运动,下列说法正确的是( )| A. | 摆球同时受到重力、拉力和向心力的作用 | |
| B. | 向心力由摆球重力和细线拉力的合力提供 | |
| C. | 摆球运动的半径越小,圆周运动的线速度越大 | |
| D. | 细线与竖直方向的夹角越大,圆周运动的周期越大 |
分析 小球受重力和拉力的合力提供向心力,结合牛顿第二定律得出线速度和周期的表达式,从而分析判断.
解答 解:A、小球做圆周运动,受到拉力和重力两个力作用,靠两个力的合力提供向心力,故A错误,B正确.
C、设绳子与竖直方向的夹角为θ,根据牛顿第二定律得:mgtanθ=m$\frac{{v}^{2}}{Lsinθ}$,解得:v=$\sqrt{gLsinθtanθ}$,半径越小,θ越小,则线速度越小,故C错误.
D、根据mgtanθ=mLsinθ•$\frac{4{π}^{2}}{{T}^{2}}$得圆周运动的周期为:T=•$2π\sqrt{\frac{Lcosθ}{g}}$,细绳与竖直方向的夹角越大,周期越小,故D错误.
故选:B.
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律进行求解,难度不大.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
2.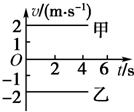 如图为甲、乙两质点的v-t图象.对于甲、乙两质点的运动,下列说法正确的是( )
如图为甲、乙两质点的v-t图象.对于甲、乙两质点的运动,下列说法正确的是( )
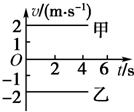 如图为甲、乙两质点的v-t图象.对于甲、乙两质点的运动,下列说法正确的是( )
如图为甲、乙两质点的v-t图象.对于甲、乙两质点的运动,下列说法正确的是( )| A. | 在相同的时间内,质点甲、乙的位移相同 | |
| B. | 质点甲和乙的速度并不相同 | |
| C. | 不管质点甲、乙是否从同一地点开始运动,它们之间的距离一定越来越大 | |
| D. | 质点甲向所选定的正方向运动,质点乙与甲的运动方向相反 |
13.假设在无风的天气里,下落的雨滴受到的空气阻力与其下落的速度成正比,假设雨滴下落的高度足够高,即雨滴着地前己达到稳定状态.则两质量比为1:2的雨滴着地前重力的瞬时功率比值为( )
| A. | 1:2 | B. | 1:4 | C. | 1:8 | D. | 1:$\sqrt{2}$ |
20.地球绕太阳和月球绕地球运行的轨道都可以近似看作是圆形的,地球和月球绕行周期之比大约是( )
| A. | 12:1 | B. | 24:1 | C. | 29:1 | D. | 30:29 |
10.利用让重物自由下落的方法“验证机械能守恒定律”,实验装置如图1所示.现有的器材为:带铁夹的铁架台、电火花打点计时器、纸带、重锤.

(1)为完成此实验,除了所给的器材,还需要的器材有AD.
A.刻度尺 B.天平 C.秒表 D.220V交流电源
(2)甲同学从打出的纸带中选出一条理想的纸带,如图2所示.选取纸带上连续打出的5个点A、B、C、D、E,测出起始点O与A点的距离为s0,A、C间的距离为s1,C、E间的距离为s2.已知重锤的质量为m,打点计时器所接交流电的频率为f,当地的重力加速度为g.从起始点O开始到打下C点的过程中,重锤重力势能的减小量为△EP=mg(s0+s1),重锤动能的增加量为△EK=$\frac{{m{{({s_1}+{s_2})}^2}{f^2}}}{32}$.在误差允许的范围内,如果△EP≈△EK,即可验证机械能守恒.
(3)乙同学经正确操作得到打点纸带,在纸带后段每两个计时间隔取一个计数点,依次为1、2、3、4、5、6、7,测量各计数点到起始点的距离h,并正确求出打相应点时的速度v.各计数点对应的数据见表:
他在如图3所示的坐标中,描点作出v2-h图线.由图线可求出重锤下落的加速度g′=9.74m/s2(保留三位有效数字);该数值明显小于当地的重力加速度,主要原因是存在摩擦和空气阻力,导致系统的机械能减少.

(1)为完成此实验,除了所给的器材,还需要的器材有AD.
A.刻度尺 B.天平 C.秒表 D.220V交流电源
(2)甲同学从打出的纸带中选出一条理想的纸带,如图2所示.选取纸带上连续打出的5个点A、B、C、D、E,测出起始点O与A点的距离为s0,A、C间的距离为s1,C、E间的距离为s2.已知重锤的质量为m,打点计时器所接交流电的频率为f,当地的重力加速度为g.从起始点O开始到打下C点的过程中,重锤重力势能的减小量为△EP=mg(s0+s1),重锤动能的增加量为△EK=$\frac{{m{{({s_1}+{s_2})}^2}{f^2}}}{32}$.在误差允许的范围内,如果△EP≈△EK,即可验证机械能守恒.
(3)乙同学经正确操作得到打点纸带,在纸带后段每两个计时间隔取一个计数点,依次为1、2、3、4、5、6、7,测量各计数点到起始点的距离h,并正确求出打相应点时的速度v.各计数点对应的数据见表:
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| h/m | 0.124 | 0.194 | 0.279 | 0.381 | 0.504 | 0.630 | 0.777 |
| v/(m•s-1) | 1.94 | 2.33 | 2.73 | 3.13 | 3.50 | ||
| v2/(m2•s-2) | 3.76 | 5.43 | 7.45 | 9.80 | 12.25 |
14. 如图所示,一群处于n=4能级的氢原子在向n=2能级跃迁过程中可能产生光子的种类有( )
如图所示,一群处于n=4能级的氢原子在向n=2能级跃迁过程中可能产生光子的种类有( )
 如图所示,一群处于n=4能级的氢原子在向n=2能级跃迁过程中可能产生光子的种类有( )
如图所示,一群处于n=4能级的氢原子在向n=2能级跃迁过程中可能产生光子的种类有( )| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
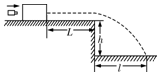 如图所示,质量为M=0.2kg的木块放在水平台面上,水平台面比水平地面高出h=0.2m,木块距水平台面的右端L=1.7m.质量为m=0.1M的子弹以v0=180m/s的速度水平射向木块,当子弹以v=90m/s的速度水平射出时,木块的速度为v1=9m/s(此过程作用时间极短,可认为木块的位移为零).若木块落到水平地面时的落地点到水平台面右端的水平距离为l=1.6m,求:(g取10m/s2)
如图所示,质量为M=0.2kg的木块放在水平台面上,水平台面比水平地面高出h=0.2m,木块距水平台面的右端L=1.7m.质量为m=0.1M的子弹以v0=180m/s的速度水平射向木块,当子弹以v=90m/s的速度水平射出时,木块的速度为v1=9m/s(此过程作用时间极短,可认为木块的位移为零).若木块落到水平地面时的落地点到水平台面右端的水平距离为l=1.6m,求:(g取10m/s2) 如图所示,两根固定的光滑硬杆OA与OB,夹角为θ,各套轻环C,D且C,D用细绳相连,现用一恒力F沿OB方向拉环C,当两环平衡时,绳子的拉力是$\frac{F}{sinθ}$.
如图所示,两根固定的光滑硬杆OA与OB,夹角为θ,各套轻环C,D且C,D用细绳相连,现用一恒力F沿OB方向拉环C,当两环平衡时,绳子的拉力是$\frac{F}{sinθ}$. 如图,在竖直平面内有一固定的光滑轨道ABCD,其中AB是长为2R的水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$圆弧轨道,两轨道相切于B点.在水平恒定拉力作用下,一质量为m的小球从A点由静止开始做匀加速直线运动,到达B点时撤除拉力.已知小球经过最高点C时对轨道的压力大小恰好为零,重力加速度大小为g.求:
如图,在竖直平面内有一固定的光滑轨道ABCD,其中AB是长为2R的水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$圆弧轨道,两轨道相切于B点.在水平恒定拉力作用下,一质量为m的小球从A点由静止开始做匀加速直线运动,到达B点时撤除拉力.已知小球经过最高点C时对轨道的压力大小恰好为零,重力加速度大小为g.求: