题目内容
14. 如图所示,在xOy坐标系原点O处有一点状的放射源,它向xOy平面内的x轴上方各个方向发射α粒子,α粒子的速度大小均为v0,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为E=$\frac{3m{v}_{0}^{2}}{2qd}$,其中q与m分别为α粒子的电量和质量;在d<y<2d的区域内有垂直于xOy平面向里的匀强磁场,mn为电场和磁场的边界线,ab为一块很大的平面感光板垂直于xOy平面且平行于x轴,放置于y=2d处,如图所示,观察发现此时恰好无粒子打到ab板上.(不考虑α粒子的重力及粒子间的相互作用).求:
如图所示,在xOy坐标系原点O处有一点状的放射源,它向xOy平面内的x轴上方各个方向发射α粒子,α粒子的速度大小均为v0,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为E=$\frac{3m{v}_{0}^{2}}{2qd}$,其中q与m分别为α粒子的电量和质量;在d<y<2d的区域内有垂直于xOy平面向里的匀强磁场,mn为电场和磁场的边界线,ab为一块很大的平面感光板垂直于xOy平面且平行于x轴,放置于y=2d处,如图所示,观察发现此时恰好无粒子打到ab板上.(不考虑α粒子的重力及粒子间的相互作用).求:(1)α粒子通过电场和磁场边界mn时距y轴的最大距离;
(2)磁感应强度B的大小;
(3)将ab板至少向下平移多大距离才能使所有的粒子均能打到板上?
分析 (1)根据动能定理求出α粒子刚进人磁场时的动能;
(2)粒子沿x轴正方向射出的粒子进入磁场偏转的角度最大,若该粒子进入磁场不能打在ab板上,则所有粒子均不能打在ab板上.根据带电粒子在电场中类平抛运动,求出进入磁场中的偏转角度,结合几何关系得出轨道半径,从而得出磁感应强度的大小;
(3)沿x轴负方向射出的粒子若能打到ab板上,则所有粒子均能打到板上.其临界情况就是此粒子轨迹恰好与ab板相切.根据带电粒子在磁场中运动的轨道半径大小得出磁场的宽度,从而确定出ab板移动的位置,根据几何关系求出ab板上被α粒子打中的区域的长度.
解答 (1)根据动能定理有:Eqd=$\frac{1}{2}$mv2-$\frac{1}{2}$m${v}_{0}^{2}$
可得:v=2v0
初速度方向与x轴平行的粒子通过边界mn时距y轴最远,由类平抛知识有:d=$\frac{1}{2}$at2
Eq=ma
x=v0t
解得:x=$\frac{2\sqrt{3}}{3}$d
(2)根据上题结果,对于沿x轴正方向射出的粒子进入磁场时与x轴正方向夹角为:θ=$\frac{π}{3}$
初速度方向与x轴平行的粒子通过边界mn时距y轴最远,而且与mn之间的夹角最小,
由图可得,若此粒子不能打到ab板上,则所有粒子均不能打到ab板,
因此此粒子轨迹与ab板相切是临界条件,可得其圆周运动的半径为:r=$\frac{2}{3}$d
又根据洛伦兹力提供向心力,有:qvB=m$\frac{{v}^{2}}{r}$
得:B=$\frac{3m{v}_{0}}{qd}$
(3)由分析可知沿x轴负方向射出的粒子若能打到ab板上,则所有粒子均能打到板上.
其临界情况就是此粒子轨迹恰好与ab板相切. 由分析可知此时磁场宽度为原来的$\frac{1}{3}$,即$\frac{1}{3}$d,
则:ab板至少向下移动:△y=$\frac{2}{3}$d
沿x轴正方向射出的粒子打在ab板的位置粒子打在ab板区域的右边界,由几何知识可知:ab板上被粒子打中区域的长度为:
L=2x+r=$\frac{4\sqrt{3}}{3}$d+$\frac{2}{3}$d
答:(1)α粒子通过电场和磁场边界mn时的速度大小及距y轴的最大距离为$\frac{2\sqrt{3}}{3}$d;
(2)磁感应强度B的大小为$\frac{3m{v}_{0}}{qd}$;
(3)将ab板至少向下平移△y=$\frac{2}{3}$d的距离才能使所有的粒子均能打到板上,此时ab板上被α粒子打中的区域的长度为$\frac{4\sqrt{3}}{3}$d+$\frac{2}{3}$d.
点评 本题考查了带电粒子在电场和磁场中的运动,关键确定粒子运动的临界情况,通过几何关系解决,对学生数学几何能力要求较高.

 智能训练练测考系列答案
智能训练练测考系列答案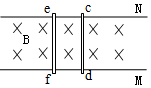 如图中M和N是两条在同一水平面内又互相平行的光滑金属导轨,ef和cd为两根金属棒,整个装置放在匀强磁场中,如果ef在外力作用下沿导轨向右运动,则通过cd的电流方向以及cd的运动方向是( )
如图中M和N是两条在同一水平面内又互相平行的光滑金属导轨,ef和cd为两根金属棒,整个装置放在匀强磁场中,如果ef在外力作用下沿导轨向右运动,则通过cd的电流方向以及cd的运动方向是( )| A. | c到d,向右 | B. | d到c,向左 | C. | c到d,向左 | D. | d到c,向右 |
 如图所示,在发射地球同步卫星的过程中,卫星首先入椭圆轨道I,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道II,则( )
如图所示,在发射地球同步卫星的过程中,卫星首先入椭圆轨道I,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道II,则( )| A. | 该卫星的发射速度必定大于11.2km/s | |
| B. | 卫星在同步轨道II上的运行速度大于7.9km/s | |
| C. | 卫星在轨道I上经过Q点的速度小于在轨道II上经过Q点的速度 | |
| D. | 卫星在轨道I上的周期大于在轨道II的周期 |
| A. | 月球质量M=$\frac{{{π}^{2}(d+2h)}^{3}}{{2GT}^{2}}$ | |
| B. | 月球探测卫星“嫦娥一号”在离月球表面h高度轨道上运行的速度v=$\frac{πd}{T}$ | |
| C. | 月球探测卫星“嫦娥一号”绕月轨道的半径r=d+h | |
| D. | 月球表面的重力加速度g=$\frac{2πd}{{T}^{2}}$ |

| A. | $\frac{{u}_{2}-{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2-t1) | |
| B. | $\frac{{u}_{2}+{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2-t1) | |
| C. | $\frac{{u}_{2}+{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2-t1) | |
| D. | $\frac{{u}_{2}-{u}_{1}}{nB{L}_{2}({t}_{2}-{t}_{1})}$ $\frac{{u}_{2}+{u}_{1}}{2nB{L}_{2}}$(t2+t1) |
| A. | 发生α衰变时,新核与原来的原子核相比,中子数减少了2 | |
| B. | 用不可见光照射金属一定比用可见光照射同种金属产生的光电子的初动能大 | |
| C. | 由玻尔理论可知,氢原子辐射出一个光子后,其电势能减小,核外电子的动能增大,原子总能量不变 | |
| D. | 比结合能小的原子核结合成或分解成比结合能大的原子核时一定放出核能 |
 a、b、c是三个质量相同的小球(可视为质点),a、b两球套在水平放置的光滑细杆上c球分别用长度为L的细线与a、b两球连接.起初a、b两球固定在细杆上相距2L处,重力加速度为g.若同时释放a、b两球,则( )
a、b、c是三个质量相同的小球(可视为质点),a、b两球套在水平放置的光滑细杆上c球分别用长度为L的细线与a、b两球连接.起初a、b两球固定在细杆上相距2L处,重力加速度为g.若同时释放a、b两球,则( )| A. | 在a、b碰撞前的任一时刻,b相对与c的速度方向与b、c的连线垂直 | |
| B. | 在a、b碰撞前的运动过程中,c的机械能先增大后减小 | |
| C. | 在a、b碰撞前的瞬间,b的速度为$\sqrt{gL}$ | |
| D. | 在a、b碰撞前的瞬间,b的速度为2$\sqrt{gL}$ |
 如图所示,有一条两岸平行,河水均匀流动、流速恒定的大河,河水流速为2$\sqrt{3}$m/s,河宽为120m.某人驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线最短.已知去程的航线AB与岸边夹角为60°,且船在静水中的速率恒定不变.求:
如图所示,有一条两岸平行,河水均匀流动、流速恒定的大河,河水流速为2$\sqrt{3}$m/s,河宽为120m.某人驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线最短.已知去程的航线AB与岸边夹角为60°,且船在静水中的速率恒定不变.求: