题目内容
17. 如图所示,质量为M的木块静止在光滑的水平面上,轻弹簧左端与木块连接,右端固定在墙壁上.一质量为m的子弹以大小为v0的速度从左端射向木块,子弹未穿出木块(子弹与木块作用时间极短).求:弹簧被压缩至最短时具有的弹性势能.
如图所示,质量为M的木块静止在光滑的水平面上,轻弹簧左端与木块连接,右端固定在墙壁上.一质量为m的子弹以大小为v0的速度从左端射向木块,子弹未穿出木块(子弹与木块作用时间极短).求:弹簧被压缩至最短时具有的弹性势能.
分析 子弹射入木块的瞬间,子弹和木块组成的系统动量守恒,根据动量守恒定律求出子弹射入木块时的共同速度.当子弹和木块系统动能为零时,弹簧压缩至最短,此时弹簧的弹性势能最大,根据能量守恒定律求出弹簧具有的最大弹性势能.
解答 解:子弹射入木块过程系统动量守恒,以向右为正方向,由动量守恒定律得:
mv0=(m+M)v,
从子弹与木块达到共同速度到弹簧压缩到最短,三者组成的系统机械能守恒,由机械能守恒定律得:
EP=$\frac{1}{2}$(m+M)v 2
解得:EP=$\frac{{m}^{2}{v}_{0}^{2}}{2(M+m)}$;
答:弹簧被压缩至最短时具有的弹性势能为$\frac{{m}^{2}{v}_{0}^{2}}{2(M+m)}$.
点评 本题综合考查了动量守恒定律和能量守恒定律,综合性较强,知道子弹射入木块后系统的动能全部转化为弹性势能时,弹性势能最大.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
8. 如图所示为研究光电效应规律的实验电路,电源的两个电极分别与接电柱c、d连接,用一定频率的单色光a照射光电管时,灵敏电流计G的指计会发生偏转,而用另一频率的单色光b照射该光电管时,灵敏电流计G的指针不偏转,下列说法正确的是( )
如图所示为研究光电效应规律的实验电路,电源的两个电极分别与接电柱c、d连接,用一定频率的单色光a照射光电管时,灵敏电流计G的指计会发生偏转,而用另一频率的单色光b照射该光电管时,灵敏电流计G的指针不偏转,下列说法正确的是( )
 如图所示为研究光电效应规律的实验电路,电源的两个电极分别与接电柱c、d连接,用一定频率的单色光a照射光电管时,灵敏电流计G的指计会发生偏转,而用另一频率的单色光b照射该光电管时,灵敏电流计G的指针不偏转,下列说法正确的是( )
如图所示为研究光电效应规律的实验电路,电源的两个电极分别与接电柱c、d连接,用一定频率的单色光a照射光电管时,灵敏电流计G的指计会发生偏转,而用另一频率的单色光b照射该光电管时,灵敏电流计G的指针不偏转,下列说法正确的是( )| A. | 用b光照射光电管时,一定没有发生光电效应 | |
| B. | a光的频率一定大于b光的频率 | |
| C. | 电源正极可能与c接线柱连接 | |
| D. | 若灵敏电流计的指针发生偏转,则电流方向有可能是由f→G→d |
5. 物体位置的变化叫位移,可以画一个从起点到终点的有向线段来表示它,线段的长度表示位移的大小.如图所示,一个跳水运动员从离水面10m高的跳台上跳起0.8米后,再落入水中,则她从起跳到入水时,通过的位移是( )
物体位置的变化叫位移,可以画一个从起点到终点的有向线段来表示它,线段的长度表示位移的大小.如图所示,一个跳水运动员从离水面10m高的跳台上跳起0.8米后,再落入水中,则她从起跳到入水时,通过的位移是( )
 物体位置的变化叫位移,可以画一个从起点到终点的有向线段来表示它,线段的长度表示位移的大小.如图所示,一个跳水运动员从离水面10m高的跳台上跳起0.8米后,再落入水中,则她从起跳到入水时,通过的位移是( )
物体位置的变化叫位移,可以画一个从起点到终点的有向线段来表示它,线段的长度表示位移的大小.如图所示,一个跳水运动员从离水面10m高的跳台上跳起0.8米后,再落入水中,则她从起跳到入水时,通过的位移是( )| A. | 11.6m | B. | 10.8m | C. | 10m | D. | 9.2m |
12.下列说法正确的是( )
| A. | 开普勒发现了行星运动的规律 | |
| B. | 卡文迪许发现了万有引力定律并用扭秤装置测出了引力常量G的数值 | |
| C. | 牛顿第一定律指出了力是维持物体运动的原因 | |
| D. | 牛顿第三定律指出了物体间的相互作用力总是大小相等、方向相反、作用线在一条直线上,作用力和反作用力的效果是可以抵消的 |
2.某同学设计了一个碰撞实验来寻找碰撞前后的不变量,实验器材有:打点计时器、低压交流电源(频率为50Hz)、纸带、表面光滑的长木板、带撞针的小车A、带橡皮泥的小车B、天平.该同学设计的实验步骤如下:
A.用天平测出小车A的质量为mA=0.4kg,小车B的质量为mB=0.2kg
B.更换纸带重复操作三次
C.小车A靠近打点计时器放置,在车后固定纸带,把小车B放在长木板中间
D.把长木板平放在桌面上,在一端固定打点计时器,连接电源
E.接通电源,并给小车A一定的初速度vA,小车A与小车B相撞黏合成一个整体
(1)请将以上步骤按操作的先后顺序排列出来ADCEB.
(2)打点计时器打下的纸带中,比较理想的一条如图所示,根据这些数据把下表空白处①②③④的数值补充完整.

(3)由表中数据可得出的结论是:碰撞前后的不变量是小车A和小车B的质量与速度的乘积(动量)之和.
A.用天平测出小车A的质量为mA=0.4kg,小车B的质量为mB=0.2kg
B.更换纸带重复操作三次
C.小车A靠近打点计时器放置,在车后固定纸带,把小车B放在长木板中间
D.把长木板平放在桌面上,在一端固定打点计时器,连接电源
E.接通电源,并给小车A一定的初速度vA,小车A与小车B相撞黏合成一个整体
(1)请将以上步骤按操作的先后顺序排列出来ADCEB.
(2)打点计时器打下的纸带中,比较理想的一条如图所示,根据这些数据把下表空白处①②③④的数值补充完整.

| 碰撞前 | 碰撞后 | ||
| 物理量 | A车 | B车 | AB整体 |
| 质量(kg) | 0.4 | 0.2 | 0.6 |
| 速度(m/s) | 3.0 | 0 | ①2.0 |
| $\frac{v}{m}$ (m•s-1•kg-1) | 7.5 | 0 | ②3.3 |
| mv (kg•m/s) | 1.2 | 0 | ③1.2 |
| mv 2 (kg•m2/s2) | 3.6 | 0 | ④2.4 |
9. 如图所示,甲、乙两球质量相同,悬线一长一短,如将两球从同一水平面无初速释放,不计阻力,则小球通过最低点时( )
如图所示,甲、乙两球质量相同,悬线一长一短,如将两球从同一水平面无初速释放,不计阻力,则小球通过最低点时( )
 如图所示,甲、乙两球质量相同,悬线一长一短,如将两球从同一水平面无初速释放,不计阻力,则小球通过最低点时( )
如图所示,甲、乙两球质量相同,悬线一长一短,如将两球从同一水平面无初速释放,不计阻力,则小球通过最低点时( )| A. | 甲球受到的拉力较乙球大 | |
| B. | 甲球的向心加速度较乙球大 | |
| C. | 甲球的动能和乙球的动能相等 | |
| D. | 相对同一参考平面,甲、乙两球的机械能一样大 |
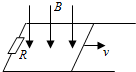 如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m的导体棒置于导轨上,在水平恒力F作用下沿导轨从静止开始向右滑动,当滑动位移为x时速度达到最大vm,滑动过程中始终保持与导轨垂直并接触良好,已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.求
如图,两平行金属导轨位于同一水平面上,相距l,左端与一电阻R相连;整个系统置于匀强磁场中,磁感应强度大小为B,方向竖直向下.一质量为m的导体棒置于导轨上,在水平恒力F作用下沿导轨从静止开始向右滑动,当滑动位移为x时速度达到最大vm,滑动过程中始终保持与导轨垂直并接触良好,已知导体棒与导轨间的动摩擦因数为μ,重力加速度大小为g,导轨和导体棒的电阻均可忽略.求 如图,固定在水平面的竖直气缸用质量不计的活塞封闭着一定质量一理想气体,一根轻绳一端系在横截面积S=160cm2的活塞中间,另一端跨过定滑轮悬挂着质量为M=80kg的重物.现气缸内气体温度从400K缓慢下降到300K,重物M被提升高度H.已知最初活塞到气缸底部的距离h=40cm,气缸外大气压强为P0=1.0×105Pa,忽略活塞与气缸壁之间的摩擦,取重力加速度的大小g=10m/s2.求
如图,固定在水平面的竖直气缸用质量不计的活塞封闭着一定质量一理想气体,一根轻绳一端系在横截面积S=160cm2的活塞中间,另一端跨过定滑轮悬挂着质量为M=80kg的重物.现气缸内气体温度从400K缓慢下降到300K,重物M被提升高度H.已知最初活塞到气缸底部的距离h=40cm,气缸外大气压强为P0=1.0×105Pa,忽略活塞与气缸壁之间的摩擦,取重力加速度的大小g=10m/s2.求