题目内容
17.有一个容积V=30L的氧气瓶,由于用气,氧气瓶中的压强由P1=50atm降到P2=30atm,温度始终保持0℃,已知标注状况下1mol气体的体积是22.4L,则使用掉的氧气分子数为多少?(已知阿伏伽德罗常数NA=6.0×1023mol-1,结果保留两位有效数字)分析 气体的温度不变,发生等温变化,根据玻意耳定律求出氧气瓶内的用掉的气体在标准状态的体积,再根据阿佛加德罗常数求出分子数即可.
解答 解:用气过程中,温度不变,根据玻意耳定律可得:p1V1=p2V2,
其中p1=50atm,p2=30atm
用掉的气体在压强是30atm时的体积为△V
△V=V2-V1=20L
设用掉的气体在标况下的体积为V3
根据玻意耳定律可得:p2△V=p0V3
其中:p0=1atm
解得:V3=600L
则用掉的气体的分子个数:n=$\frac{{V}_{3}}{{V}_{摩}}$•NA=$\frac{600}{22.4}×6.0×1{0}^{23}$个≈1.6×1025个
答:使用掉的氧气分子数约为1.6×1023个.
点评 本题考查了玻意耳定律的应用以及有关阿伏伽德罗常数的运算,注意把变质量的问题转化为定质量的问题,还要注意把体积转化成标准状态的体积.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
7. 如图所示,在xOy平面内存在这磁感应强度大小为B的匀强磁场,第一、二四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外,P(-$\sqrt{2}$L,0)、Q(0,-$\sqrt{2}$L)为坐标轴上的两个点.现有一电子从P点沿PQ方向射出,不计电子的重力,则( )
如图所示,在xOy平面内存在这磁感应强度大小为B的匀强磁场,第一、二四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外,P(-$\sqrt{2}$L,0)、Q(0,-$\sqrt{2}$L)为坐标轴上的两个点.现有一电子从P点沿PQ方向射出,不计电子的重力,则( )
 如图所示,在xOy平面内存在这磁感应强度大小为B的匀强磁场,第一、二四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外,P(-$\sqrt{2}$L,0)、Q(0,-$\sqrt{2}$L)为坐标轴上的两个点.现有一电子从P点沿PQ方向射出,不计电子的重力,则( )
如图所示,在xOy平面内存在这磁感应强度大小为B的匀强磁场,第一、二四象限内的磁场方向垂直纸面向里,第三象限内的磁场方向垂直纸面向外,P(-$\sqrt{2}$L,0)、Q(0,-$\sqrt{2}$L)为坐标轴上的两个点.现有一电子从P点沿PQ方向射出,不计电子的重力,则( )| A. | 若电子从P点出发到达原点O,则电子运动的路程一定为$\frac{πL}{2}$ | |
| B. | 若电子从P点出发到达原点O,则电子运动的路程可能为$\frac{πL}{2}$ | |
| C. | 若电子从P点出发经原点O到达Q点,则电子运动的路程一定为2πL | |
| D. | 若电子从P点出发经原点O到达Q点,则电子运动的路程可能为2πL |
5. 在三角区ABC中有垂直纸面向里的匀强磁场,如图所示.∠A=30°,在AB边界上距A点2L处的D点有一个粒子源,能沿各个方向且垂直于磁场方向发射速度大小相等带正荷的相同粒子.射到AC边上的粒子,最短时间是$\frac{1}{6}$T,T是粒子在磁场中的运动周期.关于粒子在磁场中的运动,下列说法正确的是( )
在三角区ABC中有垂直纸面向里的匀强磁场,如图所示.∠A=30°,在AB边界上距A点2L处的D点有一个粒子源,能沿各个方向且垂直于磁场方向发射速度大小相等带正荷的相同粒子.射到AC边上的粒子,最短时间是$\frac{1}{6}$T,T是粒子在磁场中的运动周期.关于粒子在磁场中的运动,下列说法正确的是( )
 在三角区ABC中有垂直纸面向里的匀强磁场,如图所示.∠A=30°,在AB边界上距A点2L处的D点有一个粒子源,能沿各个方向且垂直于磁场方向发射速度大小相等带正荷的相同粒子.射到AC边上的粒子,最短时间是$\frac{1}{6}$T,T是粒子在磁场中的运动周期.关于粒子在磁场中的运动,下列说法正确的是( )
在三角区ABC中有垂直纸面向里的匀强磁场,如图所示.∠A=30°,在AB边界上距A点2L处的D点有一个粒子源,能沿各个方向且垂直于磁场方向发射速度大小相等带正荷的相同粒子.射到AC边上的粒子,最短时间是$\frac{1}{6}$T,T是粒子在磁场中的运动周期.关于粒子在磁场中的运动,下列说法正确的是( )| A. | 垂直于AB边发射的粒子打在AC边上所用的时间最短 | |
| B. | 粒子打在AC边上的长度是$\frac{4\sqrt{3}}{3}$L-$\sqrt{3}$L | |
| C. | 粒子的轨迹半径为$\frac{2\sqrt{3}}{3}$L | |
| D. | 粒子打在AC边上的最长时间大于$\frac{1}{3}$T而小于$\frac{5}{12}$T |
9. 电荷量分别为+Q和-Q的点电荷分别固定在间距为d的M、N两点,如图所示,过MN两点连线的中点O作垂线,并以点O为圆心,$\frac{1}{3}$d为半径作圆,分别与MN连线相交于E、F,与MN连线的垂线相交于G点,下列说法正确的是( )
电荷量分别为+Q和-Q的点电荷分别固定在间距为d的M、N两点,如图所示,过MN两点连线的中点O作垂线,并以点O为圆心,$\frac{1}{3}$d为半径作圆,分别与MN连线相交于E、F,与MN连线的垂线相交于G点,下列说法正确的是( )
 电荷量分别为+Q和-Q的点电荷分别固定在间距为d的M、N两点,如图所示,过MN两点连线的中点O作垂线,并以点O为圆心,$\frac{1}{3}$d为半径作圆,分别与MN连线相交于E、F,与MN连线的垂线相交于G点,下列说法正确的是( )
电荷量分别为+Q和-Q的点电荷分别固定在间距为d的M、N两点,如图所示,过MN两点连线的中点O作垂线,并以点O为圆心,$\frac{1}{3}$d为半径作圆,分别与MN连线相交于E、F,与MN连线的垂线相交于G点,下列说法正确的是( )| A. | 圆上任意直径的两端点的电势都不等 | |
| B. | 将正点电荷分别放在圆上任意直径的两端点,受到电场力大小相等 | |
| C. | 将负点电荷放在E点比放在G点时电势能大 | |
| D. | 将负点电荷沿圆弧从F点移动到G点与从G点移动到E点,电场力做功相等 |
6.下列关于热学内容的说法正确的是( )
| A. | 减小分子之间的距离,分子斥力增大,分子引力减小 | |
| B. | 从微观角度看气体的压强与气体的平均动能和分子的密集程度有关 | |
| C. | 水蒸气的实际压强与同温度水的饱和汽压的比值叫空气的相对湿度 | |
| D. | 热量不能从低温物体传递到高温物体 | |
| E. | 一定质量的理想气体,在压强保持不变时,它的体积与绝对温度成正比 |
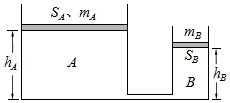 如图所示,横截面积分别为SA=30cm2与SB=10cm2的两个上部开口的柱形气缸A、B,底部通过体积可以忽略不计的细管连通,A、B气缸内分别有一个质量mA=1.0kg、mB=0.5kg的活塞,A气缸内壁粗糙,B气缸内壁光滑.当气缸内充有某种理想气体时,A、B气缸中气柱高度分别为hA=4cm、hB=3cm,此时气体温度T0=300K,外界大气压P0=1.0×105Pa.取g=10m/s2.求
如图所示,横截面积分别为SA=30cm2与SB=10cm2的两个上部开口的柱形气缸A、B,底部通过体积可以忽略不计的细管连通,A、B气缸内分别有一个质量mA=1.0kg、mB=0.5kg的活塞,A气缸内壁粗糙,B气缸内壁光滑.当气缸内充有某种理想气体时,A、B气缸中气柱高度分别为hA=4cm、hB=3cm,此时气体温度T0=300K,外界大气压P0=1.0×105Pa.取g=10m/s2.求 如图所示,第二、三象限存在足够大的匀强电场,电场强度为E,方向平行于纸面向上,一个质量为m,电量为q的正粒子,在x轴上M点(-4r,0)处以某一水平速度释放,粒子经过y轴上N点(0,2r)进入第一象限,第一象限存在一个足够大的匀强磁场,其磁感应强度B=$\sqrt{\frac{Em}{rq}}$的匀强磁场,方向如图所示,不计粒子重力,试求:
如图所示,第二、三象限存在足够大的匀强电场,电场强度为E,方向平行于纸面向上,一个质量为m,电量为q的正粒子,在x轴上M点(-4r,0)处以某一水平速度释放,粒子经过y轴上N点(0,2r)进入第一象限,第一象限存在一个足够大的匀强磁场,其磁感应强度B=$\sqrt{\frac{Em}{rq}}$的匀强磁场,方向如图所示,不计粒子重力,试求: