题目内容
20. 如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A连接,A放在光滑水平面上.有一质量为2m的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起压缩弹簧至最短;之后弹簧恢复至原长时,B与A分开沿曲面上升.下列说法正确的是( )
如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A连接,A放在光滑水平面上.有一质量为2m的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起压缩弹簧至最短;之后弹簧恢复至原长时,B与A分开沿曲面上升.下列说法正确的是( )| A. | 弹簧被压缩时所具有的最大弹性势能为$\frac{2}{3}$mgh | |
| B. | 弹簧被压缩时所具有的最大弹性势能为$\frac{4}{3}$mgh | |
| C. | B能达到的最大高度为$\frac{4}{3}$h | |
| D. | B能达到的最大高度为$\frac{4}{9}h$ |
分析 B从轨道上下滑过程,只有重力做功,机械能守恒.运用机械能守恒定律可求得B与A碰撞前的速度.两个物体碰撞过程动量守恒,即可求得碰后的共同速度.碰后共同体压缩弹簧,当速度为零,弹簧的压缩量最大,弹性势能最大,根据系统的机械能守恒求得最大的弹性势能.当弹簧再次恢复原长时,A与B将分开,根据机械能守恒求得B能达到的最大高度.
解答 解:AB、对B下滑过程,据机械能守恒定律可得:2mgh=$\frac{1}{2}•2m{v}_{0}^{2}$,
则得,B刚到达水平地面时的速度 v0=$\sqrt{2gh}$.
A碰撞过程,以A、B组成的系统为研究对象,取向右为正方向,
根据动量守恒定律可得:2mv0=3mv,
得A与B碰撞后的共同速度为 v=$\frac{2}{3}$v0,
所以弹簧被压缩时所具有的最大弹性势能为 Epm=$\frac{1}{2}$•3mv2=$\frac{4}{3}$mgh,故A错误,B正确;
CD、当弹簧再次恢复原长时,A与B将分开,B以v的速度沿斜面上滑,
根据机械能守恒定律可得 2mgh′=$\frac{1}{2}$•2mv2,
解得,B能达到的最大高度为 h′=$\frac{4}{9}h$,故C错误,D正确.
故选:BD
点评 本题考查动能定理以及动量守恒的综合运用,一定注意状态的变化和过程的分析,把动量守恒和功能关系结合起来,联立求解是常见的方法;注意反弹过程中,AB分开的条件为:AB间恰好没有弹力,而且两物体的速度恰好相同,加速度也恰好相同,故当弹簧再次变为原长时AB分开.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
11.土星的一颗卫星绕其做匀速圆周运动的半径为r,周期为T,已知引力常量为G.根据以上条件,可以求出( )
| A. | 土星的质量 | B. | 土星的密度 | ||
| C. | 卫星的角速度 | D. | 土星的表面重力加速度 |
8.如图所示,一辆小汽车沿曲面匀速运动到坡顶,该过程中( )


| A. | 小汽车所受合力总功为零 | B. | 小汽车牵引力与阻力总功为零 | ||
| C. | 小汽车所受合力做正功 | D. | 小汽车所受合力为零 |
5.下列说法中正确的是( )
| A. | 贝克勒尔通过α粒子轰击铍核的实验,发现了中子的存在 | |
| B. | 卢瑟福发现了电子并提出了原子结构的“枣糕”模型 | |
| C. | 利用玻尔理论可以准确计算出氦原子发光时放出的可见光的频率 | |
| D. | β衰变的本质是原子核内的一个中子释放一个电子变为质子 |
12.实验表明,可见光通过三棱镜时各色光的折射率n随着波长λ的变化符合科西经验公式:n=A+$\frac{B}{{λ}^{2}}$+$\frac{C}{{λ}^{4}}$,其中A、B、C是正的常量.太阳光进入三棱镜后发生色散的情形如图所示.则( )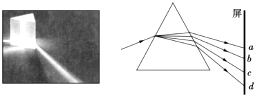

| A. | 屏上d处是紫光 | |
| B. | 屏上d处的光在棱镜中传播速度最大 | |
| C. | 屏上a处是紫光 | |
| D. | 屏上a处的光在棱镜中传播速度最小 |
14.氢原子核外电子由一个轨道向另一个轨道跃迁时,可能发生的情况是( )
| A. | 原子吸收光子,电子的动能减小,原子的电势能增大,原子的能量增大 | |
| B. | 原子吸收光子,电子的动能增大,原子的电势能减小,原子的能量增大 | |
| C. | 原子放出光子,电子的动能增大,原子的电势能减小,原子的能量减小 | |
| D. | 原子放出光子,电子的动能减小,原子的电势能增大,原子的能量减小 |
 如图所示,实线是某时刻的波形图,虚线是0.2s后的波形图.
如图所示,实线是某时刻的波形图,虚线是0.2s后的波形图.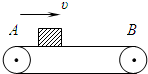 如图所示,水平传送带以v=2m/s的速度匀速运动,A、B两点相距s=11m,一质量m=1kg的物块(可视为质点)从A点由静止开始运动.已知物块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2.
如图所示,水平传送带以v=2m/s的速度匀速运动,A、B两点相距s=11m,一质量m=1kg的物块(可视为质点)从A点由静止开始运动.已知物块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2.