题目内容
11.土星的一颗卫星绕其做匀速圆周运动的半径为r,周期为T,已知引力常量为G.根据以上条件,可以求出( )| A. | 土星的质量 | B. | 土星的密度 | ||
| C. | 卫星的角速度 | D. | 土星的表面重力加速度 |
分析 卫星绕土星做匀速圆周运动,已知卫星的轨道半径和周期,根据万有引力提供向心力求解中心天体(地球)的质量,不能求解环绕天体的质量,根据圆周运动的规律可求出卫星的角速度.
解答 解:A、卫星绕土星做匀速圆周运动,根据万有引力提供向心力得 G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}r$
则有:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$,所以可求出土星的质量M,故A正确.
B、由于土星的半径未知,不能求出土星的体积,因而不能求土星的密度.故B错误.
C、根据ω=$\frac{2π}{T}$,可求得卫星的角速度,故C正确.
D、在土星表面,根据m′g=G$\frac{Mm′}{{R}^{2}}$,得土星的表面重力加速度为 g=$\frac{GM}{{R}^{2}}$,由于土星的半径求不出来,所以不能求出土星的表面重力加速,故D错误.
故选:AC
点评 解决本题的关键是掌握天体做匀速圆周运动时,由万有引力提供向心力,在天体表面,重力等于万有引力,并能灵活运用.

练习册系列答案
相关题目
1.物体在以下三个力作用下,可能做匀速直线运动的是( )
| A. | 1 N、6 N、8 N | B. | 3 N、6 N、4 N | C. | 7 N、2 N、6 N | D. | 5 N、9 N、15N |
2.一条河宽100米,船在静水中的速度为4m/s,水流速度是5m/s,则( )
| A. | 该船不可能垂直河岸横渡到对岸 | |
| B. | 过河所用的时间最短为20秒,且位移大于100米 | |
| C. | 当船头垂直河岸渡河时,船的位移最小,是100米 | |
| D. | 当船渡到对岸时,船沿河岸的最小位移是100米 |
19. 如图所示,O为等量异种点电荷连线的中点,A、B为两电荷连线中垂线上关于O点对称的两个点,关于A、B两点的场强和电势,下列说法正确的是( )
如图所示,O为等量异种点电荷连线的中点,A、B为两电荷连线中垂线上关于O点对称的两个点,关于A、B两点的场强和电势,下列说法正确的是( )
 如图所示,O为等量异种点电荷连线的中点,A、B为两电荷连线中垂线上关于O点对称的两个点,关于A、B两点的场强和电势,下列说法正确的是( )
如图所示,O为等量异种点电荷连线的中点,A、B为两电荷连线中垂线上关于O点对称的两个点,关于A、B两点的场强和电势,下列说法正确的是( )| A. | 场强和电势均相同 | B. | 场强相同,电势不同 | ||
| C. | 场强和电势均不同 | D. | 场强不同,电势相同 |
6. 如图所示,将重为G的物理课本置于水平桌面上,其$\frac{1}{3}$伸出桌外.下列说法正确的是( )
如图所示,将重为G的物理课本置于水平桌面上,其$\frac{1}{3}$伸出桌外.下列说法正确的是( )
 如图所示,将重为G的物理课本置于水平桌面上,其$\frac{1}{3}$伸出桌外.下列说法正确的是( )
如图所示,将重为G的物理课本置于水平桌面上,其$\frac{1}{3}$伸出桌外.下列说法正确的是( )| A. | 书对桌面的压力为G | |
| B. | 书对桌面的压力为$\frac{2}{3}$G | |
| C. | 书对桌面有压力是因为桌面产生了向上的形变 | |
| D. | 书对桌面有压力是因为桌面产生了向下的形变 |
16. 如图,弹簧下面挂一质量为m的物体,物体在竖直方向上做振幅为A的简谐运动,当物体振动到最高点时,弹簧正好为原长,弹簧在弹性限度内,重力加速度为g,则在物体振动过程中( )
如图,弹簧下面挂一质量为m的物体,物体在竖直方向上做振幅为A的简谐运动,当物体振动到最高点时,弹簧正好为原长,弹簧在弹性限度内,重力加速度为g,则在物体振动过程中( )
 如图,弹簧下面挂一质量为m的物体,物体在竖直方向上做振幅为A的简谐运动,当物体振动到最高点时,弹簧正好为原长,弹簧在弹性限度内,重力加速度为g,则在物体振动过程中( )
如图,弹簧下面挂一质量为m的物体,物体在竖直方向上做振幅为A的简谐运动,当物体振动到最高点时,弹簧正好为原长,弹簧在弹性限度内,重力加速度为g,则在物体振动过程中( )| A. | 物体的最大动能等于mgA | |
| B. | 弹簧的最大弹性势能等于2mgA | |
| C. | 弹簧的弹性势能和物体动能总和不变 | |
| D. | 物体在最低点时的弹力大小应为2mg |
20. 如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A连接,A放在光滑水平面上.有一质量为2m的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起压缩弹簧至最短;之后弹簧恢复至原长时,B与A分开沿曲面上升.下列说法正确的是( )
如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A连接,A放在光滑水平面上.有一质量为2m的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起压缩弹簧至最短;之后弹簧恢复至原长时,B与A分开沿曲面上升.下列说法正确的是( )
 如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A连接,A放在光滑水平面上.有一质量为2m的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起压缩弹簧至最短;之后弹簧恢复至原长时,B与A分开沿曲面上升.下列说法正确的是( )
如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A连接,A放在光滑水平面上.有一质量为2m的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起压缩弹簧至最短;之后弹簧恢复至原长时,B与A分开沿曲面上升.下列说法正确的是( )| A. | 弹簧被压缩时所具有的最大弹性势能为$\frac{2}{3}$mgh | |
| B. | 弹簧被压缩时所具有的最大弹性势能为$\frac{4}{3}$mgh | |
| C. | B能达到的最大高度为$\frac{4}{3}$h | |
| D. | B能达到的最大高度为$\frac{4}{9}h$ |
 下表是某品牌可充电电池外壳上的说明文字:该电池提供的电压是1.2V,若该电池平均工作电流为0.03A,则最多可使用20h.
下表是某品牌可充电电池外壳上的说明文字:该电池提供的电压是1.2V,若该电池平均工作电流为0.03A,则最多可使用20h.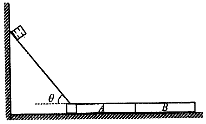 如图所示,用一块长L1=2.5m的木板(木板下端有一上表面光滑底座,其高度与木板A、B相同)在墙和地面间架设斜面,斜面与水平地面的倾角θ可在0~60°间调节后固定.将质量m1=5kg的小物块从斜面顶端静止释放,为避免小物块与地面发生撞击,在地面上紧靠轨道(的光滑底座)依次排放两块完全相同的木板A、B,长度均为l=2m,质量均为m2=10kg(忽略小物块在转角处和底座运动的能量损失).物块与斜面间的动摩擦因数μ=0.125,物块与木板间的动摩擦因数μ1=0.4,木板与地面间的动摩擦因数μ2=0.1(最大静摩擦力等于滑动摩擦力;重力加速度g=10m/s2)
如图所示,用一块长L1=2.5m的木板(木板下端有一上表面光滑底座,其高度与木板A、B相同)在墙和地面间架设斜面,斜面与水平地面的倾角θ可在0~60°间调节后固定.将质量m1=5kg的小物块从斜面顶端静止释放,为避免小物块与地面发生撞击,在地面上紧靠轨道(的光滑底座)依次排放两块完全相同的木板A、B,长度均为l=2m,质量均为m2=10kg(忽略小物块在转角处和底座运动的能量损失).物块与斜面间的动摩擦因数μ=0.125,物块与木板间的动摩擦因数μ1=0.4,木板与地面间的动摩擦因数μ2=0.1(最大静摩擦力等于滑动摩擦力;重力加速度g=10m/s2)