题目内容
6．
A、B两物体分别在水平恒力F1和F2的作用下沿水平面运动，先后撤去F1、F2后，两物体最终停下，它们的vt图象如图所示．已知两物体与水平面间的滑动摩擦力大小相等．则下列说法正确的是（ ）| A． | F1、F2大小之比为2：1 | |
| B． | F1、F2对A、B做功之比为1：2 | |
| C． | A、B质量之比为2：1 | |
| D． | 全过程中A、B克服摩擦力做功之比为2：1 |
分析 根据速度与时间的图象可知，各段运动的位移关系之比，同时由牛顿第二定律可得匀减速运动的加速度之比，再由动能定理可得出拉力、摩擦力的关系，及它们的做功关系．
解答 解：由速度与时间图象可知，两个匀减速运动的加速度之比为1：2，由牛顿第二定律可知：A、B受摩擦力大小相等，所以A、B的质量关系是2：1，
由速度与时间图象可知，A、B两物体加速与减速的位移相等，且匀加速运动位移之比1：2，匀减速运动的位移之比2：1，
由动能定理可得：A物体的拉力与摩擦力的关系，F1•X-f1•3X=0-0；B物体的拉力与摩擦力的关系，F2•2X-f2•3X=0-0，因此可得：F1=3f1，F2=$\frac{3}{2}$f2，f1=f2，所以F1=2F2．
全过程中摩擦力对A、B做功相等，F1、F2对A、B做功之大小相等．故BD错误，AC正确．
故选：AC．
点评 解决本题的关键通过图象得出匀加速运动和匀减速运动的加速度，根据牛顿第二定律，得出两个力的大小之比，以及知道速度-时间图线与时间轴所围成的面积表示位移，并运用动能定理求解．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
如图所示，一辆货车，质量为M，车上载有一箱质量为m的货物，当车辆经过长下坡路段时，司机采取挂低速挡借助发动机减速和间歇性踩刹车的方式控制车速．已知某下坡路段倾角为θ，车辆刚下坡时速度为v1，沿坡路直线向下行驶L距离后速度为v2，货物在车辆上始终未发生相对滑动，重力加速度为g，则：
17．
一列简谐横波沿直线传播，以波源O由平衡位置开始振动为计时零点，质点A的振动图象如图所示，已知O、A的平衡位置相距1.2m．以下判断正确的是（ ）
一列简谐横波沿直线传播，以波源O由平衡位置开始振动为计时零点，质点A的振动图象如图所示，已知O、A的平衡位置相距1.2m．以下判断正确的是（ ）| A． | 波速大小为0.4m/s | B． | 波源起振方向沿y轴正方向 | ||
| C． | 质点A在一个周期向前运动了1.6m | D． | 质点A的动能在t=5s时最大 |
14．硅光电池在无光照射时不产生电能，可视为一电子元件．某实验小组设计如图甲电路，给硅光电池加反向电压（硅光电池负极接高电势点，正极接低电势点），探究其在无光照时的反向伏安特性．图中电压表V1量程选用3V，内阻为6.0kΩ；电压表V2量程选用15V，内阻约为30kΩ；R0为保护电阻；直流电源电动势约为12V，内阻不计．用遮光罩罩住硅光电池，闭合开关S，调节变阻器R，读出电压表V1、V2的示数U1、U2．
（1）某次测量时，电压表V1示数如图乙，则U1=1.40V，可算出通过硅光电池的反向电流大小为0.23mA（保留两位小数）．
（2）该小组测出大量数据，筛选出下表所示的9组U1、U2数据，算出相应的硅光电池两端反向电压Ux和通过的反向电流Ix（图中“-”表示反向），并在坐标纸上建立Ix-Ux坐标系，请你标出坐标点，并绘出Ix-Ux图线．
（3）由Ix-Ux图线知，硅光电池无光照下加反向电压时，Ix与Ux成非线性（填“线性”或“非线性”）关系．
（1）某次测量时，电压表V1示数如图乙，则U1=1.40V，可算出通过硅光电池的反向电流大小为0.23mA（保留两位小数）．
（2）该小组测出大量数据，筛选出下表所示的9组U1、U2数据，算出相应的硅光电池两端反向电压Ux和通过的反向电流Ix（图中“-”表示反向），并在坐标纸上建立Ix-Ux坐标系，请你标出坐标点，并绘出Ix-Ux图线．
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| U1/V | 0.00 | 0.00 | 0.06 | 0.12 | 0.24 | 0.42 | 0.72 | 1.14 | 1.74 |
| U1/V | 0.0 | 1.0 | 2.1 | 3.1 | 4.2 | 5.4 | 6.7 | 8.1 | 9.7 |
| Ux/V | 0.0 | -1.0 | -2.0 | -3.0 | -4.0 | -5.0 | -6.0 | -7.0 | -8.0 |
| Ix/mA | -0.00 | -0.00 | -0.01 | -0.02 | -0.04 | -0.07 | -0.12 | -0.19 | -0.29 |
1．关于一定质量的物体在运动中动量、动量的变化量和加速度的关系，下列说法中不可能出现的是（ ）
| A． | 动量变化量的方向为正，加速度的方向为负 | |
| B． | 物体加速度增大，动量越来越小 | |
| C． | 动量变化越来越大，加速度反而越来越小 | |
| D． | 加速度与动量不在同一条直线上 |
11．
如图所示，某卫星S绕地球做周期为T的匀速圆周运动，地球相对卫星S的张角为θ，地球质量分布均匀的球体，其表面重力加速度为g，引力常量为G，下列说法正确的是（ ）
如图所示，某卫星S绕地球做周期为T的匀速圆周运动，地球相对卫星S的张角为θ，地球质量分布均匀的球体，其表面重力加速度为g，引力常量为G，下列说法正确的是（ ）| A． | 卫星S的轨道半径r=$\frac{{T}^{2}gsi{n}^{2}θ}{4{π}^{2}}$ | |
| B． | 卫星S的速度大小v=$\frac{Tg}{4π}$sin2$\frac{θ}{2}$ | |
| C． | 地球的密度为$\frac{3π}{G{T}^{2}si{n}^{3}\frac{θ}{2}}$ | |
| D． | 地球的第一宇宙速度大小为$\frac{Tg}{2π}$sin$\frac{θ}{2}$ |
7．关于互成角度的两个初速度不为零的匀变速直线运动的合运动，下列说法正确的是（ ）
| A． | 一定是直线运动 | B． | 一定是曲线运动 | ||
| C． | 可能是直线运动，可能是曲线运动 | D． | 一定不是曲线运动 |
4．
如图所示，一物体在沿斜面向上的恒力F作用下，由静止从底端沿光滑的斜面向上做匀加速直线运动，经过一段时间恒力F对物体做功为60J，此后撤掉力F，物体又回到出发点，在整个运动过程中下列说法正确的是（ ）
如图所示，一物体在沿斜面向上的恒力F作用下，由静止从底端沿光滑的斜面向上做匀加速直线运动，经过一段时间恒力F对物体做功为60J，此后撤掉力F，物体又回到出发点，在整个运动过程中下列说法正确的是（ ）| A． | 撤去外力时，物体的动能为60 J | |
| B． | 物体运动到最高点的过程中，重力做功为60 J | |
| C． | 物体回到出发点时，物体的动能为60 J | |
| D． | 物体回到出发点时，重力的功率出现最大值 |
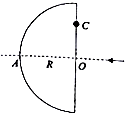如图所示是一个半径为R的半球形透明物体的侧视图，现在有一细束单色光沿半径OA方向入射，保持入射方向不变，不考虑光线在透明物体内部的反射．