��Ŀ����
2�� һ�������쳤��ϸ���ܳ����������Ϊ100N������ϸ���س����Σ�����OA�γ�Ϊ4m��OB�γ�Ϊ3m��OC�γ�Ϊ5m������������ϸ������װ��ϸɰ��СͰ��������OA��ˮƽ����ͼ��ʾ������˵����ȷ���ǣ�������
һ�������쳤��ϸ���ܳ����������Ϊ100N������ϸ���س����Σ�����OA�γ�Ϊ4m��OB�γ�Ϊ3m��OC�γ�Ϊ5m������������ϸ������װ��ϸɰ��СͰ��������OA��ˮƽ����ͼ��ʾ������˵����ȷ���ǣ�������| A�� | �����=45�㣬��OA��ϸ����OB��ϸ��������� | |
| B�� | ���cos��=0.5����OB��ϸ����OA��ϸ������������ | |
| C�� | ���ۦ����ڶ��ٶȣ�������ϸɰ��������OB��ϸ���ȶ� | |
| D�� | ���ۦ����ڶ��ٶȣ�OC��ϸ����OA��ϸ����������� |
���� ��O����������������������������ƽ��������ʽ�����õ�OA��OB�����ı���ʽ���з������ɣ�
���  �⣺��O��������������ͼ��ʾ��
�⣺��O��������������ͼ��ʾ��
����ƽ���������У�
FBcos��=FA��
FBsin��=mg��
��ã�FA=$\frac{mg}{tan��}$��${F_B}=\frac{mg}{sin��}$��
A�������=45�㣬��FA=mg��FB=$\sqrt{2}$mg����A����
B�����cos��=0.5����FA=$\frac{\sqrt{3}}{3}$mg��FB=$\frac{2}{3}\sqrt{3}$mg����OB��ϸ����OA��ϸ����������������B��ȷ��
C������${F_B}=\sqrt{F_A^2+{G^2}}$�������ۦ����ڶ��ٶȣ�������ϸɰ��������OB��ϸ���ȶϣ���C��ȷ��
D��OC���ӵ�����������������OA���ӵ�������һ��������������D����
��ѡ��BC
���� ����������ƽ�����⣬�ؼ��Ƕ�O���������������ƽ�������õ�����ʽ���з�����������Ŀ��
����ƽ��Ļ������ⷽ����
�����ĺϳɡ��ֽⷨ���������������������ij���������кϳɣ�������ת��Ϊ����������һ��ƽ���������ǰ�������ʵ��Ч�����зֽ⣬������ת��Ϊ��������������ƽ������
�����������η�������ʸ���������뼸�����������ƵĹ�ϵ����������������ķ�����Ӧ�����ַ������������յ���ݵ�Ч����

 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д� ���������ҹ��Ĵֵ������������������������ǵ�������������˼����Ӱ�죮��һ�����죬ij�˼�ʻһ��С������30m/s���ٶ���ʻ�ڸ��ٹ�·�ϣ�ͻȻ������ǰ��40m����һ��������10m/s���ٶ�ͬ����������ʻ��С��������ɲ������ɲ��������ɲ��ʧ�飮��ͼ��a��b�ֱ�ΪС�����ʹ���v-tͼ������˵����ȷ���ǣ�������
���������ҹ��Ĵֵ������������������������ǵ�������������˼����Ӱ�죮��һ�����죬ij�˼�ʻһ��С������30m/s���ٶ���ʻ�ڸ��ٹ�·�ϣ�ͻȻ������ǰ��40m����һ��������10m/s���ٶ�ͬ����������ʻ��С��������ɲ������ɲ��������ɲ��ʧ�飮��ͼ��a��b�ֱ�ΪС�����ʹ���v-tͼ������˵����ȷ���ǣ�������| A�� | ��ɲ��ʧ��ǰС�����Ѽ��٣����Բ���β | |
| B�� | ��t=5sʱ������ | |
| C�� | ��t=3sʱβ | |
| D�� | ���ڳ�ʼ����̫������ʹɲ����ʧ��Ҳ��β |
 ���õ�������ʹ�ù����У����ݲ�ʹ��ʱ������Ͽ���Դ����������ܿ��������ʹ�ٴ�ʹ��ʱ���¶Ȳ��ܼ�ʱ�ﵽҪ������ϳ�ʱ���ͨ��Դ�����˷ѵ��ܣ�Ϊ�ı����ֲ��㣬ijѧ������������װ����ͼ��ʾ�ĵ�·������R0���ʵ��Ķ�ֵ���裬R�ǵ�����������˵����ȷ���ǣ�������
���õ�������ʹ�ù����У����ݲ�ʹ��ʱ������Ͽ���Դ����������ܿ��������ʹ�ٴ�ʹ��ʱ���¶Ȳ��ܼ�ʱ�ﵽҪ������ϳ�ʱ���ͨ��Դ�����˷ѵ��ܣ�Ϊ�ı����ֲ��㣬ijѧ������������װ����ͼ��ʾ�ĵ�·������R0���ʵ��Ķ�ֵ���裬R�ǵ�����������˵����ȷ���ǣ�������| A�� | ���ݲ�ʹ�ã�Ӧ�Ͽ�S | B�� | ���ݲ�ʹ�ã�Ӧ�պ�S | ||
| C�� | ���ٴ�ʹ�ã�Ӧ�Ͽ�S | D�� | ���ٴ�ʹ�ã�Ӧ�պ�S |
| A�� | ����ij��ٶ�Ϊ8m/s | B�� | ����ij��ٶ���4m/s | ||
| C�� | ����ļ��ٶ���4m/s2 | D�� | ����ļ��ٶ���8m/s2 |

| A�� | ����Ȧ����ų������봩���ų������У���Ӧ�����ķ�����abcda���� | |
| B�� | ����Ȧ�����ų�����Ĺ����У���Ȧʼ���ܵ�ˮƽ����İ����� | |
| C�� | ����Ȧ����ų������У���Ȧ���ܾ�Ħ�����Ĺ���Ϊ$\frac{{B}^{2}{L}^{2}{v}^{2}}{R}$ | |
| D�� | ����Ȧ�����ų�����Ĺ����У��綯�������ĵĵ���Ϊ$\frac{2{B}^{2}{L}^{3}v}{R}$ |
| A�� | 1��1 | B�� | 2��1 | C�� | 3��1 | D�� | 4��1 |

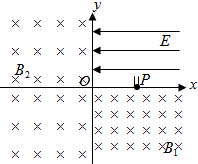 ��ͼ��ʾ����xoyƽ��ĵ�һ�����ڣ��ֲ�����x�Ḻ����ij�ǿE=$\frac{4}{3}$��104N/C����ǿ�糡�����������ڷֲ��д�ֱֽ������ĴŸ�Ӧǿ��B1����ǿ�ų����ڶ����������ڷֲ��д�ֱֽ������ĴŸ�Ӧǿ��B2����ǿ�ų�����x���Ͽ���һ��С��P��������ԭ��3cm��P��������һ�γ���d=1cm�ھ����ƣ������س鶯��ֱ�ܣ��������ھ�������û�е糡������ԴS�Թܵײ�����a���ӣ����跢���a���ٶȴ�Сv��Ϊ2��105m/s����֪a���Ӵ����磬�Ⱥ�Ϊ$\frac{q}{m}$=5��107C/kg���������ƣ���
��ͼ��ʾ����xoyƽ��ĵ�һ�����ڣ��ֲ�����x�Ḻ����ij�ǿE=$\frac{4}{3}$��104N/C����ǿ�糡�����������ڷֲ��д�ֱֽ������ĴŸ�Ӧǿ��B1����ǿ�ų����ڶ����������ڷֲ��д�ֱֽ������ĴŸ�Ӧǿ��B2����ǿ�ų�����x���Ͽ���һ��С��P��������ԭ��3cm��P��������һ�γ���d=1cm�ھ����ƣ������س鶯��ֱ�ܣ��������ھ�������û�е糡������ԴS�Թܵײ�����a���ӣ����跢���a���ٶȴ�Сv��Ϊ2��105m/s����֪a���Ӵ����磬�Ⱥ�Ϊ$\frac{q}{m}$=5��107C/kg���������ƣ��� ��ͼ��ʾ������abcdΪ������ǿ�ų����ų�������ֱ���£����αպϽ����߿���һ�����ٶ��ع⻬��Եˮƽ����ų������˶������и����������αպϽ����߿���ĸ����ܵ����λ�ã������αպϽ����߿���ٶȿ���Ϊ���λ���ǣ�������
��ͼ��ʾ������abcdΪ������ǿ�ų����ų�������ֱ���£����αպϽ����߿���һ�����ٶ��ع⻬��Եˮƽ����ų������˶������и����������αպϽ����߿���ĸ����ܵ����λ�ã������αպϽ����߿���ٶȿ���Ϊ���λ���ǣ�������


