题目内容
15.一根长为L、质量为m的均匀链条放在光滑的水平桌面上,其长度的一半悬于桌边,若要将悬着的部分拉回桌面,至少做功( )| A. | $\frac{1}{8}$mgL | B. | $\frac{1}{2}$mgL | C. | $\frac{1}{4}$mgL | D. | $\frac{1}{16}$mgL |
分析 以挂在桌边部分长为总链长的$\frac{1}{2}$链条为研究对象,在提起链条的过程中人与重力对链条做功,由动能定理可以求出人做的功.
解答 解:均匀链条的重心在其几何重心,挂在桌边部分长为总链长的$\frac{1}{2}$的链条的重心到桌面的高度为$\frac{L}{4}$.
由动能定理可得:$W{-}\frac{1}{2}mg•\frac{1}{4}{L}=\frac{1}{2}m{v^2}{-0}$,
将链条全部拉回桌面时,链条的速度为零,人所做的功最小,
W最小=$\frac{1}{8}$mgL;
故A正确,BCD错误;
故选:A
点评 该题可以选择全部的链条为研究的对象,也可以选择挂在桌边部分长为总链长的$\frac{1}{2}$为研究的对象,知道均匀项链的重心在其几何重心、应用动能定理求解变力做功.

练习册系列答案
相关题目
1.如图所示,定值电阻R1和R2分别连接在理想变压器原、副线圏上,且R1=2R2,变压器的原线圈接到交流电源上.入股变压器原、副线圈的匝数比n1:n2=1:2,则电源的输出功率是R1上消耗功率的k倍,k等于( )


| A. | 9 | B. | 8 | C. | 2 | D. | 3 |
20. 如图为一自耦变压器,原线 圈A、B端输入μ=220$\sqrt{2}$sin100πt V的正弦交流电压,副线圈电路中定值电阻R0=11Ω,所有电表均为理想电表,当原、副线圈的匝数比为10:1时( )
如图为一自耦变压器,原线 圈A、B端输入μ=220$\sqrt{2}$sin100πt V的正弦交流电压,副线圈电路中定值电阻R0=11Ω,所有电表均为理想电表,当原、副线圈的匝数比为10:1时( )
 如图为一自耦变压器,原线 圈A、B端输入μ=220$\sqrt{2}$sin100πt V的正弦交流电压,副线圈电路中定值电阻R0=11Ω,所有电表均为理想电表,当原、副线圈的匝数比为10:1时( )
如图为一自耦变压器,原线 圈A、B端输入μ=220$\sqrt{2}$sin100πt V的正弦交流电压,副线圈电路中定值电阻R0=11Ω,所有电表均为理想电表,当原、副线圈的匝数比为10:1时( )| A. | 电压表的示数为220V | B. | 电压表的示数为110$\sqrt{2}$V | ||
| C. | 电流表的示数为2A | D. | 变压器的输入功率为22W |
4.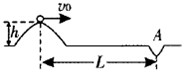 随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面的坡上水平击出一个质量为的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为的A洞.则( )
随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面的坡上水平击出一个质量为的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为的A洞.则( )
 随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面的坡上水平击出一个质量为的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为的A洞.则( )
随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面的坡上水平击出一个质量为的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为的A洞.则( )| A. | 球被击出后做平抛运动 | |
| B. | 该球从被击出到落入A洞所用的时间为$\sqrt{\frac{2h}{g}}$ | |
| C. | 球被击出时的初速度大小为L$\sqrt{\frac{g}{2h}}$ | |
| D. | 球被击出后受到的水平风力的大小$\frac{mgh}{L}$ |
5.太阳能电池已经越来越多地应用于我们生活中,有些太阳帽前安装的小风扇就是靠太阳能电池供电的.可以测得某太阳能电池的电动势为0.6V,这表示以下说法中错误的是( )
| A. | 太阳能电池在1 s内将0.6 J的太阳能转变为电能 | |
| B. | 在不接入电路时,太阳能电池两极间的电压为0.6 V | |
| C. | 电路中每通过1 C电荷量,太阳能电池把0.6 J的太阳能转变为电能 | |
| D. | 太阳能电池将太阳能转化为电能的本领比一节干电池(电动势为1.5 V)将化学能转化为电能的本领小 |
 在“探究力的平行四边形定则”的实验中,如图1所示,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.
在“探究力的平行四边形定则”的实验中,如图1所示,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳. 如图所示,在边界MN的上方存在垂直于纸面向外的匀强磁场,在边界MN的下方三角形ABD区域存在于边界向上的匀强电场,场强大小为E,AB=d,BD=2d.一质量为m、电荷量为q(q>0)的带电粒子(重力不计)从A点由静止释放,经电场加速后从B点进入磁场,最终从C点穿出电场,粒子经过C点时的速度为$\sqrt{\frac{Eqd}{m}}$.求磁场的磁感应强度的大小.
如图所示,在边界MN的上方存在垂直于纸面向外的匀强磁场,在边界MN的下方三角形ABD区域存在于边界向上的匀强电场,场强大小为E,AB=d,BD=2d.一质量为m、电荷量为q(q>0)的带电粒子(重力不计)从A点由静止释放,经电场加速后从B点进入磁场,最终从C点穿出电场,粒子经过C点时的速度为$\sqrt{\frac{Eqd}{m}}$.求磁场的磁感应强度的大小. 如图甲为倾角θ=30°的绝缘光滑匀质直角斜面体,其直角棱固定在水平地面上的光滑转动轴上,斜面长l=2m.斜面体顶端固定一个半径r=$\sqrt{3}$m的轻质绝缘光滑圆弧轨道,圆弧轨道和斜面体底边中点在同一竖直平面内,斜面体与圆弧轨道平滑连接,圆弧轨道顶端的切线方向恰好竖直.其正视图如图乙所示.圆弧轨道所在的空间区域有竖直向上的匀强电场,场强大小E=1.0×103V/m,圆弧轨道上方和下方均无电场.一个带电量q=+1.0×10-3C、质量m=0.1kg的小球(可视为质点)从斜面体底边中点处以初速度v0=$\sqrt{22}$m/s垂直底边沿斜面向上滑动,斜面体始终处于静止状态,不计空气阻力,g=10m/s2.试求:
如图甲为倾角θ=30°的绝缘光滑匀质直角斜面体,其直角棱固定在水平地面上的光滑转动轴上,斜面长l=2m.斜面体顶端固定一个半径r=$\sqrt{3}$m的轻质绝缘光滑圆弧轨道,圆弧轨道和斜面体底边中点在同一竖直平面内,斜面体与圆弧轨道平滑连接,圆弧轨道顶端的切线方向恰好竖直.其正视图如图乙所示.圆弧轨道所在的空间区域有竖直向上的匀强电场,场强大小E=1.0×103V/m,圆弧轨道上方和下方均无电场.一个带电量q=+1.0×10-3C、质量m=0.1kg的小球(可视为质点)从斜面体底边中点处以初速度v0=$\sqrt{22}$m/s垂直底边沿斜面向上滑动,斜面体始终处于静止状态,不计空气阻力,g=10m/s2.试求: