题目内容
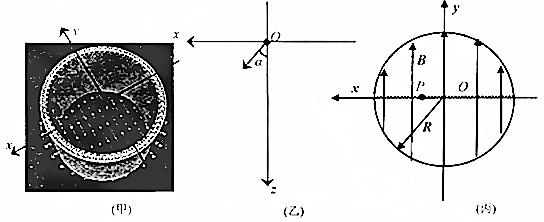
10. 如图甲为倾角θ=30°的绝缘光滑匀质直角斜面体,其直角棱固定在水平地面上的光滑转动轴上,斜面长l=2m.斜面体顶端固定一个半径r=$\sqrt{3}$m的轻质绝缘光滑圆弧轨道,圆弧轨道和斜面体底边中点在同一竖直平面内,斜面体与圆弧轨道平滑连接,圆弧轨道顶端的切线方向恰好竖直.其正视图如图乙所示.圆弧轨道所在的空间区域有竖直向上的匀强电场,场强大小E=1.0×103V/m,圆弧轨道上方和下方均无电场.一个带电量q=+1.0×10-3C、质量m=0.1kg的小球(可视为质点)从斜面体底边中点处以初速度v0=$\sqrt{22}$m/s垂直底边沿斜面向上滑动,斜面体始终处于静止状态,不计空气阻力,g=10m/s2.试求:
如图甲为倾角θ=30°的绝缘光滑匀质直角斜面体,其直角棱固定在水平地面上的光滑转动轴上,斜面长l=2m.斜面体顶端固定一个半径r=$\sqrt{3}$m的轻质绝缘光滑圆弧轨道,圆弧轨道和斜面体底边中点在同一竖直平面内,斜面体与圆弧轨道平滑连接,圆弧轨道顶端的切线方向恰好竖直.其正视图如图乙所示.圆弧轨道所在的空间区域有竖直向上的匀强电场,场强大小E=1.0×103V/m,圆弧轨道上方和下方均无电场.一个带电量q=+1.0×10-3C、质量m=0.1kg的小球(可视为质点)从斜面体底边中点处以初速度v0=$\sqrt{22}$m/s垂直底边沿斜面向上滑动,斜面体始终处于静止状态,不计空气阻力,g=10m/s2.试求:(1)小滑块能够上升到距离地面的最大高度;
(2)为使斜面体始终处于静止状态,斜面体的质量至少是多大?
分析 (1)根据已知条件判断出在圆弧轨道上做匀速圆周运动,根据几何关系求出圆心角,根据动能定理求出小滑块能够上升到距离地面的最大高度;
(2)分两种情况讨论,一是滑块在斜面顶端时,根据力矩平衡求出斜面体的质量;二是滑块在轨道顶端时,根据力矩平衡和机械能守恒定律联立求出斜面体的质量,最后综合得出结论.
解答 解:(1)由已知条件可得 qE=mg=1.0N,所以小滑块在圆弧轨道上运动时做匀速圆周运动.
由几何关系可知,圆弧轨道对应的圆心角为60°,设小滑块能够上升到距离地面的最大高度为h.由动能定理得$\frac{1}{2}mv_0^2=mg(h-rsin{60^o})$
解得h=2.6m (h>1m,答案合理)
(2)为使斜面体始终处于静止状态,设斜面体的质量至少是M.滑块在斜面上滑动时对斜面体的压力为mgcosθ,且到达斜面顶端时力臂最大,所以要使滑块在斜面上滑动时保持斜面体静止,必须满足$Mg•\frac{1}{3}lcosθ=mgcosθ•l{sin^2}θ$
解得M=0.075Kg
由qE=mg知,小滑块在圆弧轨道上做匀速圆周运动,所需的向心力等于轨道对滑块的压力.由牛顿第三定律知,滑块对轨道的压力等于向心力,且滑块在轨道顶端时对斜面体的力矩最大,所以要使滑块在圆弧轨道上做匀速圆周运动时保持斜面体静止,斜面体的质量至少满足其重力力矩等于此时滑块对轨道的压力力矩.设滑块做匀速圆周运动的速度为v,根据力矩平衡条件有$Mg\frac{1}{3}lsin{60^o}=\frac{{m{v^2}}}{r}(lsin{30^o}+rsin{60^o})$
滑块从斜面底端滑到斜面顶端过程中,由机械能守恒定律有$\frac{1}{2}mv_0^2=mglsin{30^o}+\frac{1}{2}m{v^2}$
解得 M=0.05Kg.
综上所述,M=0.075Kg
答:(1)小滑块能够上升到距离地面的最大高度2.6m;
(2)为使斜面体始终处于静止状态,斜面体的质量至少是0.075kg
点评 本题本题考查动能定理及力矩平衡和机械能守恒定律等内容,要注意正确受力分析,理清运动的过程,本题综合性很强,要能灵活运用学过的规律解题.

| A. | 通电导线受到的安培力,实质上是导体内运动电荷受到洛仑兹力的宏观表现 | |
| B. | 最先认为电磁相互作用是通过介质“场”传递的,并用“力线”描述“场”的图景的人是法拉第 | |
| C. | 磁铁周围存在磁场,是因为磁铁内有取向基本一致的分子电流 | |
| D. | 踢出去的足球最终要停下来,说明力是维持物体运动的原因 |
 在如图所示的U-I图象中,直线I为某一电源的路端电压与电流的关系图象,直线II为某一电阻R的伏安特性曲线.用该电源直接与电阻R相连组成闭合电路,由图象可知( )
在如图所示的U-I图象中,直线I为某一电源的路端电压与电流的关系图象,直线II为某一电阻R的伏安特性曲线.用该电源直接与电阻R相连组成闭合电路,由图象可知( )| A. | 电源的电动势为3 V,内阻为0.5Ω | B. | 电源的输出功率为2 W | ||
| C. | 电阻R的阻值为1Ω | D. | 电源的效率为80% |
 如图所示,两个完全相同的轻弹簧a、b,一端均固定在水平面上,另一端均与质量为m的小球相连,轻杆c一端固定在天花板上,另一端与小球相连.三者互成120°角,且两个弹簧的弹力大小均为mg.如果将轻杆突然剪断,则剪断瞬间小球的加速度大小可能为( )
如图所示,两个完全相同的轻弹簧a、b,一端均固定在水平面上,另一端均与质量为m的小球相连,轻杆c一端固定在天花板上,另一端与小球相连.三者互成120°角,且两个弹簧的弹力大小均为mg.如果将轻杆突然剪断,则剪断瞬间小球的加速度大小可能为( )| A. | a=0 | B. | a=g | C. | a=1.5g | D. | a=3g |
| A. | $\frac{1}{8}$mgL | B. | $\frac{1}{2}$mgL | C. | $\frac{1}{4}$mgL | D. | $\frac{1}{16}$mgL |

| A. | 当S与a连接后,理想电流表示数为2.2A | |
| B. | 当S与a连接后,理想电压表的示数为11V | |
| C. | 当S由a拨到b后,副线圈输出电压的频率变为25Hz | |
| D. | 当S由a拨到b后,原线圈的输入功率变为原来的4倍 |
 如图所示,在自动扶梯以恒定的速度2υ运转时,第一次有一人站到扶梯上相对扶梯静止不动,扶梯载他上楼过程中对他做功为w1,电机带动扶梯做功功率为P1,第二次这人在运动的扶梯上又以相对扶梯的速度v′同时匀速向上走,则这次扶梯对该人做功为W2,电机带动扶梯做功功率为P2以下说法中正确的是( )
如图所示,在自动扶梯以恒定的速度2υ运转时,第一次有一人站到扶梯上相对扶梯静止不动,扶梯载他上楼过程中对他做功为w1,电机带动扶梯做功功率为P1,第二次这人在运动的扶梯上又以相对扶梯的速度v′同时匀速向上走,则这次扶梯对该人做功为W2,电机带动扶梯做功功率为P2以下说法中正确的是( )| A. | W1>W2,P1>P2 | B. | W1>W2,P1=P2 | C. | W1=W2,P1>P2 | D. | W1=W2,P1=P2 |