��Ŀ����
5�� ��ͼ��ʾ��һ������̶�����ֱƽ���ڣ��ֲڵ�ab��ˮƽ�㹻����bcde�ι⻬��cde������OΪԲ�ģ��뾶ΪR=0.4m��һС��Բ������O��ab�������ϣ�����Ϊ�ʵ�����A��B������һ�𣬾�ֹ��b����mA=0.6kg��mB=0.1kg����������㹻�������������ͻȻ���룬�ֱ�������ʼ���ع���˶���B��d��ʱ�ٶ���ˮƽ����ʱ�����B��֧������С����B����������$\frac{3}{4}$��A��ab�εĶ�Ħ������Ϊ��=0.1���������ٶ�Ϊg=10m/s2����
��ͼ��ʾ��һ������̶�����ֱƽ���ڣ��ֲڵ�ab��ˮƽ�㹻����bcde�ι⻬��cde������OΪԲ�ģ��뾶ΪR=0.4m��һС��Բ������O��ab�������ϣ�����Ϊ�ʵ�����A��B������һ�𣬾�ֹ��b����mA=0.6kg��mB=0.1kg����������㹻�������������ͻȻ���룬�ֱ�������ʼ���ع���˶���B��d��ʱ�ٶ���ˮƽ����ʱ�����B��֧������С����B����������$\frac{3}{4}$��A��ab�εĶ�Ħ������Ϊ��=0.1���������ٶ�Ϊg=10m/s2������1�����B��d����ٶȴ�Сv��
��2��A��B����˲��A���ٶ�Ϊ���٣�
��3�����A�ܻ��е�������s��
���� ��1�����B��d��ʱ��������������ʽ�з��̿���ȷ����ٶ�v��
��2�����B��b��d�Ĺ��̣�ֻ���������������ݻ�е���غ㶨�����A��B����˲��B���ٶȣ����ɶ����غ㶨�����A��B����˲��A���ٶȣ�
��3�����ݶ��ܶ��������A�ܻ��е�������s��
��� �⣺��1��B��d�㣬����ţ�ٵڶ������У�mBg-$\frac{3}{4}$mBg=mB$\frac{{v}^{2}}{R}$
��ã�v=$\frac{\sqrt{gR}}{2}$=$\frac{\sqrt{10��0.4}}{2}$=1m/s
��2��B��b��d���̣�ֻ��������������е���غ㣮��
$\frac{1}{2}{m}_{B}{v}_{B}^{2}$=mBgR+$\frac{1}{2}{m}_{B}{v}^{2}$
�ã�vB=3m/s
AB������̣�ȡ����Ϊ�������ɶ����غ㶨���У�mAvA-mBvB=0
�ã�vA=0.5m/s
��3��A�ȼ���ֱ���˶����ɶ��ܶ����ã�
0-$\frac{1}{2}{m}_{A}{v}_{A}^{2}$=-��mAgs
������ã�s=0.125m
��
��1�����B��d����ٶȴ�Сv��1m/s��
��2��A��B����˲��A���ٶ�Ϊ0.5m/s��
��3�����A�ܻ��е�������s��0.125m��
���� ����Ҫ����������˶����̣�����ÿ�����̺�״̬���������ɣ���ȷ����������Դ�ǹؼ���

 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д� 2015��6��9�գ�����һ���������������������ϣ������������еĹ�ɽ��ͣס��12���˿Ͷ��ڹ�����ˣ��Դ����¹��ڿ��У������������ż������ݣ������˰��Сʱ���Ž�ȳ��������οͣ���������ɽ������֪���������е������ߵ�ʱ��û�е��ҵĸо������Ҿ������ε�������λ�ϣ�����ɽ���Ĺ���뾶R=20m��g=10m/s2��������ߵ���û�е��Ҹо�����ɽ���ٶȲ���С�ڣ�������
2015��6��9�գ�����һ���������������������ϣ������������еĹ�ɽ��ͣס��12���˿Ͷ��ڹ�����ˣ��Դ����¹��ڿ��У������������ż������ݣ������˰��Сʱ���Ž�ȳ��������οͣ���������ɽ������֪���������е������ߵ�ʱ��û�е��ҵĸо������Ҿ������ε�������λ�ϣ�����ɽ���Ĺ���뾶R=20m��g=10m/s2��������ߵ���û�е��Ҹо�����ɽ���ٶȲ���С�ڣ�������| A�� | 15.1m/s | B�� | 20.0m/s | C�� | 16.7m/s | D�� | 17.3m/s |
| A�� | a1=g1 | B�� | $\frac{{g}_{1}}{{g}_{2}}$=$\frac{{R}^{2}}{{r}^{2}}$ | C�� | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{r}{R}$ | D�� | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{r}{R}$ |
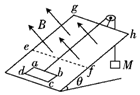 ��ͼ��ʾ���⻬б������Ϊ�ȣ���б���Ϸ���һ�����߿�abcd��ab�ߵı߳�Ϊl1��bc�ߵij�Ϊl2���߿������Ϊm������ΪR���߿�ͨ��ϸ�����������������������ΪM��б����ef�ߣ�efƽ�еױߣ����ҷ��д�ֱб�����ϵ���ǿ�ų�����l3 ��l3����l2�����Ÿ�Ӧǿ��ΪB������߿�Ӿ�ֹ��ʼ�˶���ֱ��ȫ������ų����ҽ���ų������һ��ʱ�����������˶���������˵����ȷ���ǣ�������
��ͼ��ʾ���⻬б������Ϊ�ȣ���б���Ϸ���һ�����߿�abcd��ab�ߵı߳�Ϊl1��bc�ߵij�Ϊl2���߿������Ϊm������ΪR���߿�ͨ��ϸ�����������������������ΪM��б����ef�ߣ�efƽ�еױߣ����ҷ��д�ֱб�����ϵ���ǿ�ų�����l3 ��l3����l2�����Ÿ�Ӧǿ��ΪB������߿�Ӿ�ֹ��ʼ�˶���ֱ��ȫ������ų����ҽ���ų������һ��ʱ�����������˶���������˵����ȷ���ǣ�������| A�� | �߿�abcd����ų�ǰ�˶��ļ��ٶ�Ϊ $\frac{Mg-mgsin��}{m}$ | |
| B�� | �߿��ڽ���ų������е��˶��ٶ�v=$\frac{��Mg-mgsin�ȣ�R}{{B}^{2}{{l}_{1}}^{2}}$ | |
| C�� | �߿��������˶���ʱ��Ϊ$\frac{{B}^{2}{{l}_{1}}^{2}{l}^{2}}{��Mg-mgsin�ȣ�R}$ | |
| D�� | �ù��̲����Ľ�����Q=��Mg-mgsin �ȣ�l3 |
 ��ͼ��ʾ������A��B��������Ϊm���ҷֱ����������ӿ�������֣����������뻬�֡���������֮���Ħ����������ˮƽ����F������B��ˮƽ��������������ֱ���˶��Ĺ����У�������
��ͼ��ʾ������A��B��������Ϊm���ҷֱ����������ӿ�������֣����������뻬�֡���������֮���Ħ����������ˮƽ����F������B��ˮƽ��������������ֱ���˶��Ĺ����У�������| A�� | ����AҲ������ֱ���˶� | |
| B�� | ��������ʼ�մ�������A���ܵ����� | |
| C�� | ���Ӷ�A��������С | |
| D�� | ���������B��֧���������� |
| A�� | ���� | B�� | �ٶ� | C�� | ���ٶ� | D�� | ������ |
| A�� | �����ȹ��˺� | B�� | �ɺӵ����ʱ��Ϊ16s | ||
| C�� | �ɺӵ�λ��Խ��ʱ��ҲԽ�� | D�� | �ɺӵ���Сλ��Ϊ48m |
 ���о�ƽ�������˶���ʵ���У������������¼С����˶��켣��С����ı߳�L=10���ף���С����ƽ���˶�;�еĸ���λ����ͼ�е�a��b��c��d��ʾ����С��ƽ�ij��ٶ�Ϊv0=2m/s���������������Ϊ0.1s��С����b����ֱ������ٶ�V=1.5m/s��
���о�ƽ�������˶���ʵ���У������������¼С����˶��켣��С����ı߳�L=10���ף���С����ƽ���˶�;�еĸ���λ����ͼ�е�a��b��c��d��ʾ����С��ƽ�ij��ٶ�Ϊv0=2m/s���������������Ϊ0.1s��С����b����ֱ������ٶ�V=1.5m/s��