题目内容
5.某人站在静止于光滑水平面上的平板车上,若人从车头走向车尾,人和车运动情况,下面的说法中不正确的是( )| A. | 人匀速前进,则车匀速后退 | |
| B. | 人匀加速前进,车匀加速后退,两者对地加速度大小相等 | |
| C. | 不管人如何走,任意时刻人和车动量大小总相等 | |
| D. | 人停止走动,车也静止 |
分析 根据人和车组成的系统满足动量守恒条件,根据动量守恒分析运动情况即可.
解答 解:A、根据人和车组成的系统动量守恒有:mv+Mv′=0可得,可知人与车速度的大小与质量成反比,故人匀速前进,则车匀速后退,故A正确;
B、人对车的作用力和车对人的作用力互为作用力与反作用力,故其大小相等方向相反,若人的质量和车的质量相等,则此时人的加速度和车的加速度大小相等,故B不正确;
C、因为人和车组成的系统水平方向动量守恒,故不管人如何走动,人和车的总动量等于开始时的动量0,所以任意时刻人和车动量大小总相等,方向相反.故C正确;
D、由C分析知,人和车的总动量等于开始时的动量,而开始时人和车均静止,故当人静止时,车也静止,故D正确.
本题选不正确的,故选:B.
点评 掌握人和车组成的系统满足动量守恒条件,根据动量守恒定律进行分析结论即可,注意人和车产生的加速度由相互之间的作用力产生,故加速度的大小与质量成反比.

练习册系列答案
相关题目
20.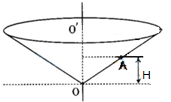 如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )
如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )
 如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )
如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )| A. | $\sqrt{\frac{g}{2H}}$ | B. | $\sqrt{\frac{5g}{8H}}$ | C. | $\sqrt{\frac{3g}{2H}}$ | D. | $\sqrt{\frac{2g}{H}}$ |
10. 在高处以初速度v1水平抛出一个带刺飞镖,在离开抛出点水平距离 l、2l处有A、B两个小气球以速度v2匀速上升,先后被飞镖刺破(认为飞镖质量很大,刺破气球不会改变其平抛运动的轨迹).则下列判断正确的是( )
在高处以初速度v1水平抛出一个带刺飞镖,在离开抛出点水平距离 l、2l处有A、B两个小气球以速度v2匀速上升,先后被飞镖刺破(认为飞镖质量很大,刺破气球不会改变其平抛运动的轨迹).则下列判断正确的是( )
 在高处以初速度v1水平抛出一个带刺飞镖,在离开抛出点水平距离 l、2l处有A、B两个小气球以速度v2匀速上升,先后被飞镖刺破(认为飞镖质量很大,刺破气球不会改变其平抛运动的轨迹).则下列判断正确的是( )
在高处以初速度v1水平抛出一个带刺飞镖,在离开抛出点水平距离 l、2l处有A、B两个小气球以速度v2匀速上升,先后被飞镖刺破(认为飞镖质量很大,刺破气球不会改变其平抛运动的轨迹).则下列判断正确的是( )| A. | 飞镖刺破A气球时,飞镖的速度大小为vA=$\frac{gl}{{v}_{1}}$ | |
| B. | 飞镖刺破A气球时,飞镖的速度大小为vA=$\sqrt{{{v}_{1}}^{2}+\frac{{g}^{2}{l}^{2}}{{{v}_{1}}^{2}}}$ | |
| C. | A、B两个小气球未被刺破前的匀速上升过程中,高度差为$\frac{3g{l}^{2}}{2{{v}_{1}}^{2}}$ | |
| D. | A、B两个小气球未被刺破前的匀速上升过程中,高度差为$\frac{3g{l}^{2}}{2{{v}_{1}}^{2}}$+$\frac{{v}_{2}l}{{v}_{1}}$ |
14. 用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的直径.如图所示,在ab的左侧存在一个匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0),则( )
用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的直径.如图所示,在ab的左侧存在一个匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0),则( )
 用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的直径.如图所示,在ab的左侧存在一个匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0),则( )
用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的直径.如图所示,在ab的左侧存在一个匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0),则( )| A. | 圆环具有缩小的趋势 | |
| B. | 圆环中产生顺时针方向的感应电流 | |
| C. | 圆环中感应电流的大小为$\frac{krS}{2ρ}$ | |
| D. | 图中a、b两点之间的电势差UAB=|$\frac{1}{4}$kπr2| |

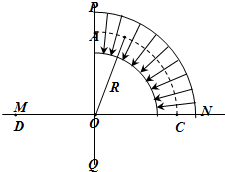 如图所示,MN为绝缘板,PQ为MN的中垂线,O为MN的中点,在MN的下方有匀强磁场,磁场方向垂直纸面向外(图中未画出),质量为m电荷量为q的粒子(不计重力)以某一速度从A点平行于MN的方向进入静电分析器,静电分析器内有均匀辐向分布的电场(电场方向指向O点),已知圆弧虚线的半径为R,其所在处场强为E,若离子恰好沿图中虚线做圆周运动后从小孔C垂直于MN进入下方磁场.
如图所示,MN为绝缘板,PQ为MN的中垂线,O为MN的中点,在MN的下方有匀强磁场,磁场方向垂直纸面向外(图中未画出),质量为m电荷量为q的粒子(不计重力)以某一速度从A点平行于MN的方向进入静电分析器,静电分析器内有均匀辐向分布的电场(电场方向指向O点),已知圆弧虚线的半径为R,其所在处场强为E,若离子恰好沿图中虚线做圆周运动后从小孔C垂直于MN进入下方磁场. 如图所示,外电路在电场力的作用下,移动2C电荷电场力做功12J,在整个闭合回路中,移动1C电荷做功8J,R1:R3=3:1,安培表1的示数为1A,求电源电动势和内电阻.
如图所示,外电路在电场力的作用下,移动2C电荷电场力做功12J,在整个闭合回路中,移动1C电荷做功8J,R1:R3=3:1,安培表1的示数为1A,求电源电动势和内电阻. 图甲所示线圈总电阻r=0.5Ω,匝数n=10,其端点a、b与R=1.5Ω的电阻相连,线圈内磁通量变化规律如图乙所示.关于a、b两点电势ϕa大于ϕb(填“大于”或“小于”),两点电势差Uab=1.5V.
图甲所示线圈总电阻r=0.5Ω,匝数n=10,其端点a、b与R=1.5Ω的电阻相连,线圈内磁通量变化规律如图乙所示.关于a、b两点电势ϕa大于ϕb(填“大于”或“小于”),两点电势差Uab=1.5V.


