题目内容
13.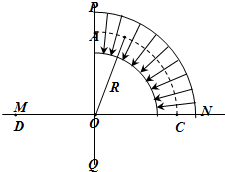 如图所示,MN为绝缘板,PQ为MN的中垂线,O为MN的中点,在MN的下方有匀强磁场,磁场方向垂直纸面向外(图中未画出),质量为m电荷量为q的粒子(不计重力)以某一速度从A点平行于MN的方向进入静电分析器,静电分析器内有均匀辐向分布的电场(电场方向指向O点),已知圆弧虚线的半径为R,其所在处场强为E,若离子恰好沿图中虚线做圆周运动后从小孔C垂直于MN进入下方磁场.
如图所示,MN为绝缘板,PQ为MN的中垂线,O为MN的中点,在MN的下方有匀强磁场,磁场方向垂直纸面向外(图中未画出),质量为m电荷量为q的粒子(不计重力)以某一速度从A点平行于MN的方向进入静电分析器,静电分析器内有均匀辐向分布的电场(电场方向指向O点),已知圆弧虚线的半径为R,其所在处场强为E,若离子恰好沿图中虚线做圆周运动后从小孔C垂直于MN进入下方磁场.(1)求粒子运动的速度大小;
(2)粒子在磁场中运动,与MN板碰撞,碰后以原速率反弹,且碰撞时无电荷的转移,之后恰好从小孔D进入MN上方的三角形匀强磁场中,从A点平行于MC射出,OC=OD,则三角形磁场区域最小面积为多少?MN上下两区域磁场的磁感应强度之比为多少?
(3)在(2)问情景下,求粒子从A点出发后,第一次回到A点所经过的总时间为多少?
分析 (1)粒子在静电分析器中做匀速圆周运动,电场力提供向心力,由向心力与速度之间的关系式,即可求得粒子的速度大小.
(2)做出粒子的运动的轨迹图,结合数学知识可求得三角形区域的磁场的最小面积;在磁场中洛伦兹力提供向心力,在MN上方和下方分别列示可求得磁感应强度的比值.
(3)把这个运动分成三个阶段,分别是在第一象限、第二象限和第三四象限,分别求出三个阶段的时间,即可求得第一次回到A点所经过的总时间.
解答 解:(1)粒子进入静电分析器做圆周运动,故有:qE=$\frac{m{V}^{2}}{R}$
解得:V=$\sqrt{\frac{qER}{m}}$
(2)粒子从D到A匀速圆周运动,故由图示三角形区域面积最小值为:S=$\frac{{R}^{2}}{2}$
在磁场中洛伦兹力提供向心力,有:qVB=$\frac{m{V}^{2}}{R}$
解得:R=$\frac{mV}{qB}$ 设MN下方的磁感应强度为B1,上方的磁感应强度为B2,
设MN下方的磁感应强度为B1,上方的磁感应强度为B2,
若只碰撞一次,则有:
R1=$\frac{R}{2}$=$\frac{mV}{q{B}_{1}}$,
R2=R=$\frac{mV}{q{B}_{2}}$,
解得:$\frac{{B}_{2}}{{B}_{1}}$=$\frac{1}{2}$
若碰撞n次,则有:
R1=$\frac{R}{n+1}$=$\frac{mV}{q{B}_{1}}$
R2=R=$\frac{mV}{q{B}_{2}}$
故有:$\frac{{B}_{2}}{{B}_{1}}$=$\frac{1}{n+1}$
(3)粒子在电场中运动时间为:
t1=$\frac{2πR}{4V}$=$\frac{π}{2}\sqrt{\frac{mR}{qE}}$
在MN下方的磁场中运动时间为:
t2=$\frac{n+1}{2}$×2πR1×$\frac{1}{V}$=$πR\sqrt{\frac{m}{qER}}$
在MN上方的磁场中运动时间为:
t3=$\frac{1}{4}$×$\frac{2π{R}_{2}}{V}$=$\frac{π}{2}\sqrt{\frac{mR}{qE}}$
总时间为:
t=t1+t2+t3=2π$\sqrt{\frac{mR}{qE}}$
答:(1)求粒子运动的速度大小为$\sqrt{\frac{qER}{m}}$;
(2)粒子在磁场中运动,与MN板碰撞,碰后以原速率反弹,且碰撞时无电荷的转移,之后恰好从小孔D进入MN上方的三角形匀强磁场中,从A点平行于MC射出,OC=OD,则三角形磁场区域最小面积为$\frac{{R}^{2}}{2}$,MN上下两区域磁场的磁感应强度之比为$\frac{1}{n+1}$
(3)在(2)问情景下,求粒子从A点出发后,第一次回到A点所经过的总时间为2π$\sqrt{\frac{mR}{qE}}$.
点评 对于带电粒子在磁场的中的运动,可以进行如下的归类进行解析:
1、带电粒子在匀强磁场中匀速圆周运动基本问题
找圆心、画轨迹是解题的基础.带电粒子垂直于磁场进入一匀强磁场后在洛伦兹力作用下必作匀速圆周运动,抓住运动中的任两点处的速度,分别作出各速度的垂线,则二垂线的交点必为圆心;或者用垂径定理及一处速度的垂线也可找出圆心;再利用数学知识求出圆周运动的半径及粒子经过的圆心角从而解答物理问题.
2、带电粒子在磁场中轨道半径变化问题
导致轨道半径变化的原因有:①带电粒子速度变化导致半径变化.如带电粒子穿过极板速度变化;带电粒子使空气电离导致速度变化;回旋加速器加速带电粒子等.②磁场变化导致半径变化.如通电导线周围磁场,不同区域的匀强磁场不同;磁场随时间变化.③动量变化导致半径变化.如粒子裂变,或者与别的粒子碰撞;④电量变化导致半径变化.如吸收电荷等.总之,由r=$\frac{mv}{qB}$看m、v、q、B中某个量或某两个量的乘积或比值的变化就会导致带电粒子的轨道半径变化.
3、带电粒子在磁场中运动的临界问题和带电粒子在多磁场中运动问题
带电粒子在磁场中运动的临界问题的原因有:粒子运动范围的空间临界问题;磁场所占据范围的空间临界问题,运动电荷相遇的时空临界问题等.审题时应注意恰好,最大、最多、至少等关键字
4、带电粒子在有界磁场中的极值问题
寻找产生极值的条件:①直径是圆的最大弦;②同一圆中大弦对应大的圆心角;③由轨迹确定半径的极值.
5、带电粒子在复合场中运动问题
复合场包括:磁场和电场,磁场和重力场,或重力场、电场和磁场.有带电粒子的平衡问题,匀变速运动问题,非匀变速运动问题,在解题过程中始终抓住洛伦兹力不做功这一特点.粒子动能的变化是电场力或重力做功的结果.
6、带电粒子在磁场中的周期性和多解问题
多解形成原因:带电粒子的电性不确定形成多解;磁场方向不确定形成多解;临界状态的不唯一形成多解,在有界磁场中运动时表现出来多解,运动的重复性形成多解.

 阅读快车系列答案
阅读快车系列答案| A. | 关于光的本性,牛顿提出了“微粒说”,惠更斯提出了“波动说”,爱因斯坦提出了“光子说”,综合他们的说法圆满地说明了光的本性 | |
| B. | 光具有波粒二象性是指既可以把光看成宏观概念上的波,也可以看成微观概念上的粒子 | |
| C. | 光的干涉、衍射现象说明光具有波动性,光电效应和康普顿效应说明光具有粒子性 | |
| D. | 频率低、波长长的光,粒子性特征显著;频率高、波长短的光,波动性特征显著 |
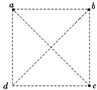 在光滑的绝缘水平面上,有一个正方形abcd,顶点a、c 处分别固定一个正点电荷,电荷量相等,如图所示.若将一个带负电的粒子在b点自由释放,粒子将沿着对角线bd往复运动.则在粒子从b点运动到d点的过程中( )
在光滑的绝缘水平面上,有一个正方形abcd,顶点a、c 处分别固定一个正点电荷,电荷量相等,如图所示.若将一个带负电的粒子在b点自由释放,粒子将沿着对角线bd往复运动.则在粒子从b点运动到d点的过程中( )| A. | 先做匀加速运动,后做匀减速运动 | |
| B. | 先从高电势到低电势,后从低电势到高电势 | |
| C. | 电势能与机械能之和保持不变 | |
| D. | 电势能先增大后减小 |
| A. | 人匀速前进,则车匀速后退 | |
| B. | 人匀加速前进,车匀加速后退,两者对地加速度大小相等 | |
| C. | 不管人如何走,任意时刻人和车动量大小总相等 | |
| D. | 人停止走动,车也静止 |
| A. | 任何核反应,只要伴随能量的产生,则反应前后各物质的质量和一定不相等 | |
| B. | 太阳不断地向外辐射能量,因而太阳的总质量一定不断减小 | |
| C. | 虽然太阳不断地向外辐射能量,但它的总质量是不可改变的 | |
| D. | 若地球从太阳获得的能量大于地球向外辐射的能量,则地球的质量将不断增大 |
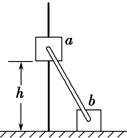 如图,滑块a、b的质量均为m=1kg,a套在固定竖直杆上,与光滑水平地面相距h=0.2m,b放在地面上.a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点.
如图,滑块a、b的质量均为m=1kg,a套在固定竖直杆上,与光滑水平地面相距h=0.2m,b放在地面上.a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点.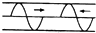 从一条弦线的两端,各发出一如图所示的脉冲横波,它们均沿弦线传播,速度相等,传播方向相反,在它们传播过程中,可能出现的脉冲波形是下图中( )
从一条弦线的两端,各发出一如图所示的脉冲横波,它们均沿弦线传播,速度相等,传播方向相反,在它们传播过程中,可能出现的脉冲波形是下图中( )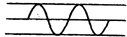

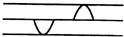
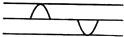
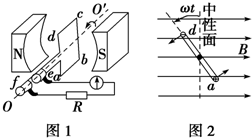 图1是交流发电机模型示意图.在磁感应强度为B的匀强磁场中,有一矩形线圈abcd可绕线圈平面内垂直于磁感线的轴OO′转动,由线圈引出的导线ae和df分别与两个跟线圈一起绕OO′转动的金属圆环相连接,金属圆环又分别与两个固定的电刷保持滑动接触,这样矩形线圈在转动中就可以保持和外电路电阻R形成闭合电路.图2是线圈的主视图,导线ab和cd分别用它们的横截面来表示.已知ab长度为L1,bc长度为L2,线圈以恒定角速度ω逆时针转动.(只考虑单匝线圈)
图1是交流发电机模型示意图.在磁感应强度为B的匀强磁场中,有一矩形线圈abcd可绕线圈平面内垂直于磁感线的轴OO′转动,由线圈引出的导线ae和df分别与两个跟线圈一起绕OO′转动的金属圆环相连接,金属圆环又分别与两个固定的电刷保持滑动接触,这样矩形线圈在转动中就可以保持和外电路电阻R形成闭合电路.图2是线圈的主视图,导线ab和cd分别用它们的横截面来表示.已知ab长度为L1,bc长度为L2,线圈以恒定角速度ω逆时针转动.(只考虑单匝线圈)