��Ŀ����
8�� ��ͼ��ʾ������OO���Ҳ���ڴ�ֱ��ֽ������Ÿ�Ӧǿ��ΪB����ǿ�ų���ijʱ������Ϊm�������Ϊ-q��q��0��������a��ֽ�������ٶ�v1=v0��A�����ų����䷽����OO��ļнǦ�1=30�㣻��һ����Ϊm�������Ϊ+q������b��ֽ�������ٶ�v2=$\sqrt{3}$v0Ҳ��A������ų����䷽����OO��ļнǦ�2=60�㣮��֪����a��bͬʱ����ų��߽��P��Q���㣨ͼ��δ���������������ӵ����������Ӽ������ã�
��ͼ��ʾ������OO���Ҳ���ڴ�ֱ��ֽ������Ÿ�Ӧǿ��ΪB����ǿ�ų���ijʱ������Ϊm�������Ϊ-q��q��0��������a��ֽ�������ٶ�v1=v0��A�����ų����䷽����OO��ļнǦ�1=30�㣻��һ����Ϊm�������Ϊ+q������b��ֽ�������ٶ�v2=$\sqrt{3}$v0Ҳ��A������ų����䷽����OO��ļнǦ�2=60�㣮��֪����a��bͬʱ����ų��߽��P��Q���㣨ͼ��δ���������������ӵ����������Ӽ������ã���1���������ӽ���ų���ʱ������t��
��2�����������ڴų��߽��ϵĴ�����֮��ľ���d��
���� ��1�����������ӵ��˶��켣���ɼ��ι�ϵ����켣��Ӧ��Բ�ĽǦȣ����ݹ�ʽt=$\frac{��}{2��}$T������������ڴų����˶���ʱ�䣬�ɡ�t=t1-t2��⣮
��2����ţ�ٵڶ���������뾶����ϼ���֪ʶ���d��
���  ��������1������Բ���˶������� T=$\frac{2��m}{qB}$
��������1������Բ���˶������� T=$\frac{2��m}{qB}$
����aԲ���˶���Բ�Ľ� ��=$\frac{5��}{3}$����ǿ�ų����˶���ʱ�� t1=$\frac{��}{2��}$T��
����bԲ���˶���Բ�Ľ� ��=$\frac{4��}{3}$������ǿ�ų����˶���ʱ�� t2=$\frac{��}{2��}$T
��֪����a��bͬʱ����ų��߽��P��Q���㣬���ԡ�t=t1-t2=$\frac{��m}{3qB}$
��2����������ǿ�ų���������Բ���˶�������ţ�ٵڶ�������
qvB=m$\frac{{v}_{0}^{2}}{r}$���� r=$\frac{m{v}_{0}}{qB}$
������a�ӱ߽��ϵ�C���뿪�ų�����AC=2 r1 sin��1
������b�ӱ߽��ϵ�D���뿪�ų�����AD=2r2 sin��2
��d=AC+AD=2r1 sin30��+2r2sin60��=$\frac{4m{v}_{0}}{qB}$
��
��1�������ӽ���ų���ʱ������tΪ$\frac{��m}{3qB}$��
��2���������ڴų��߽��ϵĴ�����֮��ľ���dΪ$\frac{4m{v}_{0}}{qB}$��
���� �����dz����Ĵ��������ڴų����˶������⣬�����켣�����ü���֪ʶ�Ǵ������������ڴų����˶�����Ļ���������

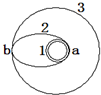 ��ͼ��ʾ����ij�η����������ǵ�ʾ��ͼ�������������ڰ뾶Ϊr�Ľ���Բ�ܹ��1���˶���Ȼ�������Բ���2���˶�������ڰ뾶Ϊ7r��Բ�ܹ��3���˶���a���ǹ��1��2�Ľ��㣬b���ǹ��2��3�Ľ��㣬���������ڹ��1��a����ٶ�Ϊv1a���ڹ��2��a����ٶ�Ϊv2a���ڹ��2��b����ٶ�Ϊv2b���ڹ��3��b����ٶ�Ϊv3b����֪������Բ�������ʱ����������ΪEp=-$\frac{GMm}{r}$��ѡ������Զ��Ϊ������㣬r��������������������ľ࣬����˵����ȷ���ǣ�������
��ͼ��ʾ����ij�η����������ǵ�ʾ��ͼ�������������ڰ뾶Ϊr�Ľ���Բ�ܹ��1���˶���Ȼ�������Բ���2���˶�������ڰ뾶Ϊ7r��Բ�ܹ��3���˶���a���ǹ��1��2�Ľ��㣬b���ǹ��2��3�Ľ��㣬���������ڹ��1��a����ٶ�Ϊv1a���ڹ��2��a����ٶ�Ϊv2a���ڹ��2��b����ٶ�Ϊv2b���ڹ��3��b����ٶ�Ϊv3b����֪������Բ�������ʱ����������ΪEp=-$\frac{GMm}{r}$��ѡ������Զ��Ϊ������㣬r��������������������ľ࣬����˵����ȷ���ǣ�������| A�� | ���1��2��3������֮��Ϊ7$\sqrt{7}$��8��1 | |
| B�� | v2a��v1a��v2b��v3b | |
| C�� | v1a��v2a��v3b��v2b | |
| D�� | Բ�ܹ��1��3������ʱ�����Ǻ͵���ϵͳ�Ļ�е��֮��Ϊ7��1 |
| A�� | ���ڴ��������У��ʵ����Ƶ�ʵ��ڲ�Դ����Ƶ�� | |
| B�� | ��ij����������������ЧӦʱ����Ӧ��Դ����Ƶ��һ�������仯 | |
| C�� | ������������ʱ��������Ƶ��Խ�ߣ��������������Խ�� | |
| D�� | ����˹̹���������ָ��������еĹ����ڲ�ͬ�Ĺ��Բο�ϵ�ж�����ͬ�� | |
| E�� | X���ߵ�Ƶ�ʱ����ߵ粨��Ƶ�ʸ� |
 ��ͼ��ʾ������б��⻬�Ӵ�����ˮƽ����F�����ƶ�б��ʹ������A�ˣ���ʱ���ӽӽ�ˮƽλ�ã����ڴ˹����У����ӵ�����ΪT�����б���ѹ��ΪN��������
��ͼ��ʾ������б��⻬�Ӵ�����ˮƽ����F�����ƶ�б��ʹ������A�ˣ���ʱ���ӽӽ�ˮƽλ�ã����ڴ˹����У����ӵ�����ΪT�����б���ѹ��ΪN��������| A�� | N��������T�ȼ�С������ | B�� | N��������T���ϼ�С | ||
| C�� | N���䣬T�������� | D�� | N���䣬T�ȼ�С������ |
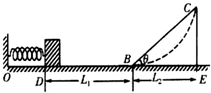 ��ͼ��һ̽�����ܹ�ϵ��ʵ��װ�ã�ˮƽ����б�潻��B�㣬�ᵯ����˹̶�����ֱǽ�棬������Ϊm�Ļ���ѹ��������D�㣬�ɾ�ֹ�ͷţ��������뵯�ɺ�ǡ���ܻ���б����ߵ�C��Ȼ��ȥ��б�����Բ���ι�����û�������ͬλ��D��ֹ�ͷţ�������Բ�����������ij�㣮��֪ˮƽ�桢б��BC��Բ���ι���ͻ����Ķ�Ħ��������Ϊ�̣�BD=L1��б��ױ�BE=L2�����Ϊ�ȣ��������Ϊ�ʵ㣬���ƻ�����B��Ļ�е����ʧ��������
��ͼ��һ̽�����ܹ�ϵ��ʵ��װ�ã�ˮƽ����б�潻��B�㣬�ᵯ����˹̶�����ֱǽ�棬������Ϊm�Ļ���ѹ��������D�㣬�ɾ�ֹ�ͷţ��������뵯�ɺ�ǡ���ܻ���б����ߵ�C��Ȼ��ȥ��б�����Բ���ι�����û�������ͬλ��D��ֹ�ͷţ�������Բ�����������ij�㣮��֪ˮƽ�桢б��BC��Բ���ι���ͻ����Ķ�Ħ��������Ϊ�̣�BD=L1��б��ױ�BE=L2�����Ϊ�ȣ��������Ϊ�ʵ㣬���ƻ�����B��Ļ�е����ʧ��������| A�� | �ͷŻ���ǰ���ɵĵ�������Ϊ��mg��L1+L2��+mgL2tan�� | |
| B�� | ������D�㻬��B��ʱ����Ϊ��mgL2+mgL2tan�� | |
| C�� | �������˶������л��������ĸ߶���ͬ | |
| D�� | �������˶������л���Ļ�е����ʧ��Ϊ��mg��L1+$\frac{{L}_{2}}{cos��}$�� |

| A�� | ͨ��L1�ĵ�����СΪͨ��L2������2�� | |
| B�� | L1���ĵĵ繦��Ϊ0.75W | |
| C�� | L2���ĵĵ繦��ԼΪ0.19W | |
| D�� | L2�ĵ���Ϊ6�� |
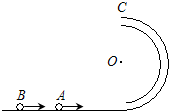 ��ͼ��ʾ���뾶ΪR���ھ���С�Ĺ⻬��Բϸ����ֱ���ã�����������Ϊm��С��A��B���Բ�ͬ�����ʽ�����ڣ���A��ͨ��Բ����ߵ�C���Թܱ��ϲ���ѹ��Ϊ3mg��B��ͨ����ߵ�Cʱ���Թܱ��ڡ�����ѹ����Ϊ0����A��B����ص��ľ��룮
��ͼ��ʾ���뾶ΪR���ھ���С�Ĺ⻬��Բϸ����ֱ���ã�����������Ϊm��С��A��B���Բ�ͬ�����ʽ�����ڣ���A��ͨ��Բ����ߵ�C���Թܱ��ϲ���ѹ��Ϊ3mg��B��ͨ����ߵ�Cʱ���Թܱ��ڡ�����ѹ����Ϊ0����A��B����ص��ľ��룮 ��ͼ��ʾ��С��A�ڹ⻬�İ뾶ΪR��Բ�β���������Բ���˶��������˶���ͼ�е�a��ʱ����Բ�β�����O�����Ϸ�h������һС��B��0a������ijһ����ˮƽ�׳������ǡ����a����A��������g=10m/s2��
��ͼ��ʾ��С��A�ڹ⻬�İ뾶ΪR��Բ�β���������Բ���˶��������˶���ͼ�е�a��ʱ����Բ�β�����O�����Ϸ�h������һС��B��0a������ijһ����ˮƽ�׳������ǡ����a����A��������g=10m/s2��