题目内容
3. 如图所示,小球A在光滑的半径为R的圆形槽内作匀速圆周运动,当它运动到图中的a点时,在圆形槽中心O点正上方h处,有一小球B沿0a方向以某一初速水平抛出,结果恰好在a点与A球相碰,g=10m/s2求
如图所示,小球A在光滑的半径为R的圆形槽内作匀速圆周运动,当它运动到图中的a点时,在圆形槽中心O点正上方h处,有一小球B沿0a方向以某一初速水平抛出,结果恰好在a点与A球相碰,g=10m/s2求(1)B球抛出时的水平初速多大?
(2)A球运动的线速度最小值为多大?
(3)若考虑到匀速圆周运动是周期性运动,A球速度满足什么条件,两球就能在a点相碰?
分析 根据高度求出平抛运动的时间,根据水平位移和时间求出B球平抛运动的初速度.抓住时间相等,结合线速度与周期的关系求出线速度的最小值.
解答 解:(1)根据h=$\frac{1}{2}$gt2得,
t=$\sqrt{\frac{2h}{g}}$,
则B球抛出的初速度v0=$\frac{R}{t}$=$R\sqrt{\frac{g}{2h}}$,
(2)当A球转动一圈和小球B相碰,此时A球转动的线速度最小,
则有:$\frac{2πR}{v}$=t=$\sqrt{\frac{2h}{g}}$,
解得最小线速度v=$2πR\sqrt{\frac{g}{2h}}$;
(3)只要在B球落至a点时A球同时也到达a点即相碰.考虑到A球运动的周期性,
所以有$\frac{2kπR}{v}$=$\sqrt{\frac{2h}{g}}$,
由此解得v=2kπR$\sqrt{\frac{g}{2h}}$ (k=1,2,3,…).
答:(1)B球抛出时的水平初速是$R\sqrt{\frac{g}{2h}}$,
(2)A球运动的线速度最小值为$2πR\sqrt{\frac{g}{2h}}$;
(3)若考虑到匀速圆周运动是周期性运动,A球速度满足v=2kπR$\sqrt{\frac{g}{2h}}$ (k=1,2,3,…),两球就能在a点相碰.
点评 解决本题的关键知道平抛运动的时间由高度决定,两球相遇,时间相等,注意A球运动的周期性.

练习册系列答案
相关题目
5. 如图所示的电路中,电源电动势为E、内阻忽略不计,ab是总电阻为2R的滑动变阻器,滑片P刚开始位于中间位置,定值电阻的阻值为R,平行板电容器的电容为C,其下极板与地(取为零电势)相连,一电量为q带正电的粒子固定在两板中央e处,闭合开关S,待稳定后,下列判断正确的是( )
如图所示的电路中,电源电动势为E、内阻忽略不计,ab是总电阻为2R的滑动变阻器,滑片P刚开始位于中间位置,定值电阻的阻值为R,平行板电容器的电容为C,其下极板与地(取为零电势)相连,一电量为q带正电的粒子固定在两板中央e处,闭合开关S,待稳定后,下列判断正确的是( )
 如图所示的电路中,电源电动势为E、内阻忽略不计,ab是总电阻为2R的滑动变阻器,滑片P刚开始位于中间位置,定值电阻的阻值为R,平行板电容器的电容为C,其下极板与地(取为零电势)相连,一电量为q带正电的粒子固定在两板中央e处,闭合开关S,待稳定后,下列判断正确的是( )
如图所示的电路中,电源电动势为E、内阻忽略不计,ab是总电阻为2R的滑动变阻器,滑片P刚开始位于中间位置,定值电阻的阻值为R,平行板电容器的电容为C,其下极板与地(取为零电势)相连,一电量为q带正电的粒子固定在两板中央e处,闭合开关S,待稳定后,下列判断正确的是( )| A. | e处的电势为$\frac{1}{6}$E | |
| B. | 若把滑片P移至b端,稳定后粒子的电势能减少了$\frac{1}{3}$Eq | |
| C. | 若把滑片P移至b端,稳定后粒子所受电场力变为原来的2倍 | |
| D. | 若把滑片P移至b端,同时上极板向上移动仅使板间距变为原来的2倍,稳定后电容器的带电量变为原来的1.5倍 |
11.在物理学发展的过程中,许多科学家的科学研究推动了人类文明的进程.在对以下几位科学家所作贡献的叙述正确的是( )
| A. | 天文学家第谷提出太阳系行星运动三大定律 | |
| B. | 物理学家牛顿提出了万有引力定律并给出了万有引力常量的值 | |
| C. | 卡文迪许用实验的方法测出万有引力常量G | |
| D. | 亚当斯和勒维耶各自独立依据万有引力定律计算出了天王星的轨道,故人们称其为“笔尖下发现的行星” |
18. 如图所示,有一平行板电容器充电后带有等量异种电荷,然后与电源断开.下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两极板左右水平错开一段很小的距离,则下列说法中正确的是( )
如图所示,有一平行板电容器充电后带有等量异种电荷,然后与电源断开.下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两极板左右水平错开一段很小的距离,则下列说法中正确的是( )
 如图所示,有一平行板电容器充电后带有等量异种电荷,然后与电源断开.下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两极板左右水平错开一段很小的距离,则下列说法中正确的是( )
如图所示,有一平行板电容器充电后带有等量异种电荷,然后与电源断开.下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两极板左右水平错开一段很小的距离,则下列说法中正确的是( )| A. | 电容器两极板间电压值变大 | B. | 电荷的电势能变大 | ||
| C. | 负电荷所在处的电势升高 | D. | 电容器两极板间的电场强度变小 |
15.对于相互接触的两个物体之间,同一接触面上的弹力和摩擦力,以下说法中正确的是( )
| A. | 有弹力必有摩擦力 | B. | 有摩擦力必有弹力 | ||
| C. | 摩擦力的大小一定与弹力成正比 | D. | 摩擦力的方向一定与运动方向相反 |
12.据每日邮报2014年4月18日报道,美国国家航空航天局(NASA)目前宣布首次在太阳系外发现“类地”行星Kepler-186f.假如宇航员乘坐宇宙飞船到达该行星,进行科学观测:该行星自转周期为T;宇航员在该行星“北极”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t1;宇航员在该行星“赤道”距该行星地面附近h处自由释放-个小球(引力视为恒力),落地时间为t2.则行星的半径R的值( )
| A. | R=$\frac{({{t}_{2}}^{2}+{{t}_{1}}^{2})h{T}^{2}}{4{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| B. | R=$\frac{({{t}_{2}}^{2}+{{t}_{1}}^{2})h{T}^{2}}{2{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| C. | R=$\frac{({{t}_{2}}^{2}-{{t}_{1}}^{2})h{T}^{2}}{2{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ | |
| D. | R=$\frac{({{t}_{2}}^{2}-{{t}_{1}}^{2})h{T}^{2}}{4{π}^{2}{{t}_{1}}^{2}{{t}_{2}}^{2}}$ |
 如图所示,小物块A、B由跨过定滑轮的轻绳相连,A置于倾角为37°的光滑固定斜面上,B位于水平传送带的左端,轻绳分别与斜面、传送带平行.传送带始终以速度v0=2m/s顺时针匀速传动,某时刻B从传送带左端以速度v1=6m/s向右运动,经一段时间回到传送带的左端.已知A、B质量均为1kg,B与传送带间的动摩擦因数为μ=0.2,斜面、轻绳、传送带均足够长,A不会碰到定滑轮,定滑轮的质量与摩擦均不计.g取10m/s2,sin37°=0.6.求:
如图所示,小物块A、B由跨过定滑轮的轻绳相连,A置于倾角为37°的光滑固定斜面上,B位于水平传送带的左端,轻绳分别与斜面、传送带平行.传送带始终以速度v0=2m/s顺时针匀速传动,某时刻B从传送带左端以速度v1=6m/s向右运动,经一段时间回到传送带的左端.已知A、B质量均为1kg,B与传送带间的动摩擦因数为μ=0.2,斜面、轻绳、传送带均足够长,A不会碰到定滑轮,定滑轮的质量与摩擦均不计.g取10m/s2,sin37°=0.6.求: 如图所示,虚线OO′右侧存在垂直于纸面向里、磁感应强度为B的匀强磁场,某时候质量为m、电荷量为-q(q>0)的粒子a在纸面内以速度v1=v0从A点进入磁场,其方向与OO′的夹角θ1=30°;另一质量为m、电荷量为+q的粒子b在纸面内以速度v2=$\sqrt{3}$v0也从A点射入磁场,其方向与OO′的夹角θ2=60°.已知粒子a、b同时到达磁场边界的P、Q两点(图中未画出),不计粒子的重力及粒子间的相互作用.
如图所示,虚线OO′右侧存在垂直于纸面向里、磁感应强度为B的匀强磁场,某时候质量为m、电荷量为-q(q>0)的粒子a在纸面内以速度v1=v0从A点进入磁场,其方向与OO′的夹角θ1=30°;另一质量为m、电荷量为+q的粒子b在纸面内以速度v2=$\sqrt{3}$v0也从A点射入磁场,其方向与OO′的夹角θ2=60°.已知粒子a、b同时到达磁场边界的P、Q两点(图中未画出),不计粒子的重力及粒子间的相互作用.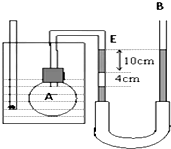 如图所示为验证查理定律的实验装置.A为烧瓶,内贮空气.B为U形管,下部与较长的软橡胶管相连.由于组装不慎,U形管左侧10cm水银柱的下方混入一段长为4cm的空气柱,左侧水银柱上表面与标志线E对齐.开始时烧瓶所在水槽内水温为7℃,U形管两边水银面相平.当水温升至63℃时,调整右边开口水银管的高度,使左侧水银柱上表面仍与标志线E对齐.已知大气压p0=76cmHg.此时:
如图所示为验证查理定律的实验装置.A为烧瓶,内贮空气.B为U形管,下部与较长的软橡胶管相连.由于组装不慎,U形管左侧10cm水银柱的下方混入一段长为4cm的空气柱,左侧水银柱上表面与标志线E对齐.开始时烧瓶所在水槽内水温为7℃,U形管两边水银面相平.当水温升至63℃时,调整右边开口水银管的高度,使左侧水银柱上表面仍与标志线E对齐.已知大气压p0=76cmHg.此时: