题目内容
19.一根铁链总长为L,平放在桌面上,铁链每单位长度的质量为λ.现用手提起链的一端,使之以速度v竖直地匀速上升,试求在从一端离地开始到全链恰离地,手的拉力的冲量$\frac{λg{L}^{2}}{2v}$+λLv.分析 本题采用微元法进行分析,设其中一小段为研究对象,由动量定理可分析手的拉力的动量.
解答  解:图示是链的一微元段离地的情景,则该段微元长为:
解:图示是链的一微元段离地的情景,则该段微元长为:
△x=$\frac{L}{n}$(n→∞)
该段微元质量△m=λ•△x;
设该元段从静止到被提起历时△t,那么竖直上升部分长x的链条在手的拉力F,重力的冲量作用下,发生了末段微元动量的变化,由动量定理:
(F-λxg)△t=△mv
F-λxg=$\frac{△x}{△t}$λv=λv2
解得:F=λv2+λxg=λv2+λgvt+t∈[0,$\frac{L}{v}$]
力随时间线性变化,故可由数学规律可知整个过程手拉力F的总冲量:
I=(λv2+$\frac{λgL}{2}$)•$\frac{L}{v}$=$\frac{λg{L}^{2}}{2v}$+λLv
故答案为:$\frac{λg{L}^{2}}{2v}$+λLv
点评 本题用到微分原理及来分析动量定理,要求学生对数学中的微元法掌握的较准确才能求解.属于考查数学规律在物理中的应用难度较大的题目.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
1.以下说法正确的是( )
| A. | 一定质量的气体,在体积不变时,分子每秒与器壁平均碰撞次数随着温度降低而减小 | |
| B. | 晶体熔化时吸收热量,分子平均动能一定增大 | |
| C. | 知道水蒸气的摩尔体积和水分子的体积,可计算出阿伏加德罗常数 | |
| D. | 当分子间的引力和斥力平衡时,分子势能最小 |
11.在物理学发展的过程中,许多科学家的科学研究推动了人类文明的进程.在对以下几位科学家所作贡献的叙述正确的是( )
| A. | 天文学家第谷提出太阳系行星运动三大定律 | |
| B. | 物理学家牛顿提出了万有引力定律并给出了万有引力常量的值 | |
| C. | 卡文迪许用实验的方法测出万有引力常量G | |
| D. | 亚当斯和勒维耶各自独立依据万有引力定律计算出了天王星的轨道,故人们称其为“笔尖下发现的行星” |
9.以下说法正确的是( )
| A. | 卢瑟福通过α粒子散射实验提出了原子核式结构的模型 | |
| B. | 麦克斯韦首先从实验上证实了电磁波的存在 | |
| C. | 爱因斯坦提出“光子”理论,成功地对光电效应进行了解释 | |
| D. | 在相对论中,运动中的时钟会比静止时走得快 |

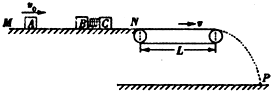 如图所示为某种弹射装置的示意图,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度L=4.0m,皮带轮沿顺时针方向转动,带动皮带以恒定速率v=3.0m/s匀速传动.三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上,开始时滑块B、C之间用细绳相连,中间有一压缩的轻弹簧,处于静止状态,滑块A以初速度v0=2.0m/s沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短,可认为A与B碰撞过程中滑块C的速度仍为零.因碰撞使连接B、C的细绳受扰动而突然断开,弹簧伸展,从而使C与A、B分离.滑块C脱离弹簧后以速度 vC=2.0m/s滑上传送带,并从右端滑出落至地面上的P点,已知滑块C与传送带之间的动摩擦因数μ=0.20,重力加速度g取10m/s2.求:
如图所示为某种弹射装置的示意图,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度L=4.0m,皮带轮沿顺时针方向转动,带动皮带以恒定速率v=3.0m/s匀速传动.三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上,开始时滑块B、C之间用细绳相连,中间有一压缩的轻弹簧,处于静止状态,滑块A以初速度v0=2.0m/s沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短,可认为A与B碰撞过程中滑块C的速度仍为零.因碰撞使连接B、C的细绳受扰动而突然断开,弹簧伸展,从而使C与A、B分离.滑块C脱离弹簧后以速度 vC=2.0m/s滑上传送带,并从右端滑出落至地面上的P点,已知滑块C与传送带之间的动摩擦因数μ=0.20,重力加速度g取10m/s2.求: 如图所示,小物块A、B由跨过定滑轮的轻绳相连,A置于倾角为37°的光滑固定斜面上,B位于水平传送带的左端,轻绳分别与斜面、传送带平行.传送带始终以速度v0=2m/s顺时针匀速传动,某时刻B从传送带左端以速度v1=6m/s向右运动,经一段时间回到传送带的左端.已知A、B质量均为1kg,B与传送带间的动摩擦因数为μ=0.2,斜面、轻绳、传送带均足够长,A不会碰到定滑轮,定滑轮的质量与摩擦均不计.g取10m/s2,sin37°=0.6.求:
如图所示,小物块A、B由跨过定滑轮的轻绳相连,A置于倾角为37°的光滑固定斜面上,B位于水平传送带的左端,轻绳分别与斜面、传送带平行.传送带始终以速度v0=2m/s顺时针匀速传动,某时刻B从传送带左端以速度v1=6m/s向右运动,经一段时间回到传送带的左端.已知A、B质量均为1kg,B与传送带间的动摩擦因数为μ=0.2,斜面、轻绳、传送带均足够长,A不会碰到定滑轮,定滑轮的质量与摩擦均不计.g取10m/s2,sin37°=0.6.求: 如图所示,虚线OO′右侧存在垂直于纸面向里、磁感应强度为B的匀强磁场,某时候质量为m、电荷量为-q(q>0)的粒子a在纸面内以速度v1=v0从A点进入磁场,其方向与OO′的夹角θ1=30°;另一质量为m、电荷量为+q的粒子b在纸面内以速度v2=$\sqrt{3}$v0也从A点射入磁场,其方向与OO′的夹角θ2=60°.已知粒子a、b同时到达磁场边界的P、Q两点(图中未画出),不计粒子的重力及粒子间的相互作用.
如图所示,虚线OO′右侧存在垂直于纸面向里、磁感应强度为B的匀强磁场,某时候质量为m、电荷量为-q(q>0)的粒子a在纸面内以速度v1=v0从A点进入磁场,其方向与OO′的夹角θ1=30°;另一质量为m、电荷量为+q的粒子b在纸面内以速度v2=$\sqrt{3}$v0也从A点射入磁场,其方向与OO′的夹角θ2=60°.已知粒子a、b同时到达磁场边界的P、Q两点(图中未画出),不计粒子的重力及粒子间的相互作用.