题目内容
16.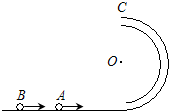 如图所示,半径为R,内径很小的光滑半圆细管竖直放置,两个质量均为m的小球A、B,以不同的速率进入管内,若A球通过圆周最高点C,对管壁上部的压力为3mg,B球通过最高点C时,对管壁内、外侧的压力均为0,求A、B球落地点间的距离.
如图所示,半径为R,内径很小的光滑半圆细管竖直放置,两个质量均为m的小球A、B,以不同的速率进入管内,若A球通过圆周最高点C,对管壁上部的压力为3mg,B球通过最高点C时,对管壁内、外侧的压力均为0,求A、B球落地点间的距离.
分析 对两个球分别受力分析,根据合力提供向心力,由牛顿第二定律求出两球通过C点的速度,再据平抛运动求出落地的距离.
解答 解:A小球在最高点时,受重力和管壁的作用力,这两个力的合力作为向心力.
对A球:3mg+mg=m$\frac{{v}_{A}^{2}}{R}$
解得:vA=2$\sqrt{gR}$ ①
对B球:mg=m$\frac{{v}_{B}^{2}}{R}$
解得:vB=$\sqrt{gR}$ ②
AB 两球从最高点做平抛运动,据平抛运动得:2R=$\frac{1}{2}g{t}^{2}$ ③
A、B球落地点间的距离△x=(vA-vB)t ④
联立①②③④解得:△x=2R
答:A、B球落地点间的距离2R.
点评 该题考查向心力,解题的关键是对小球在最高点处时受力分析,然后根据向心力公式和牛顿第二定律求出速度;再据平抛运动求出距离.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在物理学发展的过程中,许多科学家的科学研究推动了人类文明的进程.在对以下几位科学家所作贡献的叙述正确的是( )
| A. | 天文学家第谷提出太阳系行星运动三大定律 | |
| B. | 物理学家牛顿提出了万有引力定律并给出了万有引力常量的值 | |
| C. | 卡文迪许用实验的方法测出万有引力常量G | |
| D. | 亚当斯和勒维耶各自独立依据万有引力定律计算出了天王星的轨道,故人们称其为“笔尖下发现的行星” |
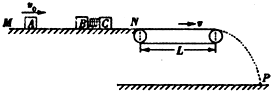 如图所示为某种弹射装置的示意图,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度L=4.0m,皮带轮沿顺时针方向转动,带动皮带以恒定速率v=3.0m/s匀速传动.三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上,开始时滑块B、C之间用细绳相连,中间有一压缩的轻弹簧,处于静止状态,滑块A以初速度v0=2.0m/s沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短,可认为A与B碰撞过程中滑块C的速度仍为零.因碰撞使连接B、C的细绳受扰动而突然断开,弹簧伸展,从而使C与A、B分离.滑块C脱离弹簧后以速度 vC=2.0m/s滑上传送带,并从右端滑出落至地面上的P点,已知滑块C与传送带之间的动摩擦因数μ=0.20,重力加速度g取10m/s2.求:
如图所示为某种弹射装置的示意图,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度L=4.0m,皮带轮沿顺时针方向转动,带动皮带以恒定速率v=3.0m/s匀速传动.三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上,开始时滑块B、C之间用细绳相连,中间有一压缩的轻弹簧,处于静止状态,滑块A以初速度v0=2.0m/s沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短,可认为A与B碰撞过程中滑块C的速度仍为零.因碰撞使连接B、C的细绳受扰动而突然断开,弹簧伸展,从而使C与A、B分离.滑块C脱离弹簧后以速度 vC=2.0m/s滑上传送带,并从右端滑出落至地面上的P点,已知滑块C与传送带之间的动摩擦因数μ=0.20,重力加速度g取10m/s2.求:



 如图所示,虚线OO′右侧存在垂直于纸面向里、磁感应强度为B的匀强磁场,某时候质量为m、电荷量为-q(q>0)的粒子a在纸面内以速度v1=v0从A点进入磁场,其方向与OO′的夹角θ1=30°;另一质量为m、电荷量为+q的粒子b在纸面内以速度v2=$\sqrt{3}$v0也从A点射入磁场,其方向与OO′的夹角θ2=60°.已知粒子a、b同时到达磁场边界的P、Q两点(图中未画出),不计粒子的重力及粒子间的相互作用.
如图所示,虚线OO′右侧存在垂直于纸面向里、磁感应强度为B的匀强磁场,某时候质量为m、电荷量为-q(q>0)的粒子a在纸面内以速度v1=v0从A点进入磁场,其方向与OO′的夹角θ1=30°;另一质量为m、电荷量为+q的粒子b在纸面内以速度v2=$\sqrt{3}$v0也从A点射入磁场,其方向与OO′的夹角θ2=60°.已知粒子a、b同时到达磁场边界的P、Q两点(图中未画出),不计粒子的重力及粒子间的相互作用. 如图,一个物体静止放在水平面上,在跟竖直方向成θ角为37度的斜向下的推力F=20N的作用下沿水平移动的距离s=5m,若物体的质量为m=0.4kg,物体与地面之间的动摩擦因数μ=0.2,(g=10m/s2,sin37.=0.6,cos37.=0.8)求:
如图,一个物体静止放在水平面上,在跟竖直方向成θ角为37度的斜向下的推力F=20N的作用下沿水平移动的距离s=5m,若物体的质量为m=0.4kg,物体与地面之间的动摩擦因数μ=0.2,(g=10m/s2,sin37.=0.6,cos37.=0.8)求: 在“研究平抛物体运动”的实验中:
在“研究平抛物体运动”的实验中: