题目内容
3.物体与倾斜角为α的斜面间的动摩擦因数为μ,当物体沿斜面以初速度V0从底部沿斜面向上冲时,所能达到的最大高度是?分析 根据牛顿第二定律求出物体上滑的加速度大小,结合速度位移公式求出上滑的最大距离,从而得出物体能达到的最大高度.
解答 解:根据牛顿第二定律得,物体上滑的加速度大小a=$\frac{mgsinα+μmgcosα}{m}$=gsinα+μgcosα,
则物体上滑的最大距离x=$\frac{{{v}_{0}}^{2}}{2a}=\frac{{{v}_{0}}^{2}}{2(gsinα+μgcosα)}$,
则物体能达到的最大高度h=xsinα=$\frac{{{v}_{0}}^{2}sinα}{2g(sinα+μcosα)}$.
答:物体能达到的最大高度为$\frac{{{v}_{0}}^{2}sinα}{2g(sinα+μcosα)}$.
点评 本题考查了牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁,难度不大.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
10.关于地磁场,下列说法正确的是( )
| A. | 地磁场的N极在地球的南极附近 | |
| B. | 北京地区地磁场方向由北向南 | |
| C. | 地球周围的磁感线从地球地理南极附近出发,回到地球地理北极附近 | |
| D. | 在地磁南(S)极处,可以自由转动的小磁针的N极竖直指向地面 |
11.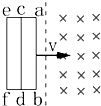 如图所示矩形金属框架的三条竖直边ab、cd、ef长均为L,电阻都为R,其余电阻不计,框架以速度v匀速地进入磁感应强度为B的匀强磁场中,设ab、cd、ef三条边先后进入磁场时,ab边两端的电压分别为U1,U2,和U3,则( )
如图所示矩形金属框架的三条竖直边ab、cd、ef长均为L,电阻都为R,其余电阻不计,框架以速度v匀速地进入磁感应强度为B的匀强磁场中,设ab、cd、ef三条边先后进入磁场时,ab边两端的电压分别为U1,U2,和U3,则( )
 如图所示矩形金属框架的三条竖直边ab、cd、ef长均为L,电阻都为R,其余电阻不计,框架以速度v匀速地进入磁感应强度为B的匀强磁场中,设ab、cd、ef三条边先后进入磁场时,ab边两端的电压分别为U1,U2,和U3,则( )
如图所示矩形金属框架的三条竖直边ab、cd、ef长均为L,电阻都为R,其余电阻不计,框架以速度v匀速地进入磁感应强度为B的匀强磁场中,设ab、cd、ef三条边先后进入磁场时,ab边两端的电压分别为U1,U2,和U3,则( )| A. | U1=$\frac{BLv}{3}$ | B. | U2=2U1 | C. | U3=0 | D. | U1=U2=U3 |
8.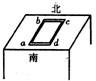 根据地磁场的特征可知,在北半球的地磁场有一水平向北的分量Bx和一个竖直向下的分量By,某研究性小组设计了如图所示实验测量Bx和By的大小,将一个电阻为R的长方形线圈abcd沿着磁针所指的南北方向平放在北半球的一个水平桌面上,测得线圈两边的长度为ab=L1,bc=L2,现突然将线圈翻转180°,使ab边与dc边互换位置,用冲击电流计测得线圈中流过的电荷量为q1,然后维持bc边不动,将线圈绕bc边转动,使线圈突然竖直,这次测得线圈中流过的电荷量为q2,则( )
根据地磁场的特征可知,在北半球的地磁场有一水平向北的分量Bx和一个竖直向下的分量By,某研究性小组设计了如图所示实验测量Bx和By的大小,将一个电阻为R的长方形线圈abcd沿着磁针所指的南北方向平放在北半球的一个水平桌面上,测得线圈两边的长度为ab=L1,bc=L2,现突然将线圈翻转180°,使ab边与dc边互换位置,用冲击电流计测得线圈中流过的电荷量为q1,然后维持bc边不动,将线圈绕bc边转动,使线圈突然竖直,这次测得线圈中流过的电荷量为q2,则( )
 根据地磁场的特征可知,在北半球的地磁场有一水平向北的分量Bx和一个竖直向下的分量By,某研究性小组设计了如图所示实验测量Bx和By的大小,将一个电阻为R的长方形线圈abcd沿着磁针所指的南北方向平放在北半球的一个水平桌面上,测得线圈两边的长度为ab=L1,bc=L2,现突然将线圈翻转180°,使ab边与dc边互换位置,用冲击电流计测得线圈中流过的电荷量为q1,然后维持bc边不动,将线圈绕bc边转动,使线圈突然竖直,这次测得线圈中流过的电荷量为q2,则( )
根据地磁场的特征可知,在北半球的地磁场有一水平向北的分量Bx和一个竖直向下的分量By,某研究性小组设计了如图所示实验测量Bx和By的大小,将一个电阻为R的长方形线圈abcd沿着磁针所指的南北方向平放在北半球的一个水平桌面上,测得线圈两边的长度为ab=L1,bc=L2,现突然将线圈翻转180°,使ab边与dc边互换位置,用冲击电流计测得线圈中流过的电荷量为q1,然后维持bc边不动,将线圈绕bc边转动,使线圈突然竖直,这次测得线圈中流过的电荷量为q2,则( )| A. | By=$\frac{R{q}_{1}}{{L}_{1}{L}_{2}}$ | B. | By=$\frac{R{q}_{1}}{2{L}_{1}{L}_{2}}$ | ||
| C. | Bx=$\frac{R(2{q}_{2}+{q}_{1})}{2{L}_{1}{L}_{2}}$ | D. | Bx=$\frac{R(2{q}_{2}-{q}_{1})}{2{L}_{1}{L}_{2}}$ |
12.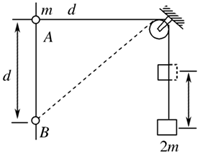 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑的轻小定滑轮与直杆的距离为d,杆上的A点与定滑轮等高,杆上的B点在A点下方距离为d处.现将环从A处由静止释放,不计一切摩擦阻力,下列说法正确的是( )| A. | 环到达B处时,重物上升的高度h=$\sqrt{2}d$ | |
| B. | 环到达B处时,环与重物的速度大小满足${v_物}=\sqrt{2}{v_环}$ | |
| C. | 环到达B,重物的速度大小${v_物}=\frac{{\sqrt{(6-4\sqrt{2})gd}}}{2}$ | |
| D. | 环从A到达B的过程中,环克服轻绳拉力做的功($\sqrt{2}$-1)mgd |
13.质量为m的物体,在距地面为h的高处,以$\frac{2g}{3}$的恒定加速度由静止竖直下落到地面,对于这一下落过程中,下列说法中正确的是( )
| A. | 物体的重力势能减少$\frac{mgh}{3}$ | B. | 物体的机械能减少$\frac{2mgh}{3}$ | ||
| C. | 物体的动能增加$\frac{2mgh}{3}$ | D. | 重力做功$\frac{2mgh}{3}$ |
 如图,光滑平行金属导轨置于水平面上,AB、CD两导体直棒相互平行横置于导轨上,匀强磁场方向竖直向上,当导体棒AB向右移动时,CD将如何运动?
如图,光滑平行金属导轨置于水平面上,AB、CD两导体直棒相互平行横置于导轨上,匀强磁场方向竖直向上,当导体棒AB向右移动时,CD将如何运动?
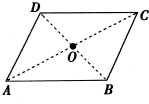 在一匀强电场区域中,有A、B、C、D四点恰好位于一平行四边形的四个顶点上,如图所示,O点为平行四边形两条对角线的交点,已知:φA=-4V,φB=6V,φC=8V,则D、O两点电势φD的为-2V,φO的为2V.
在一匀强电场区域中,有A、B、C、D四点恰好位于一平行四边形的四个顶点上,如图所示,O点为平行四边形两条对角线的交点,已知:φA=-4V,φB=6V,φC=8V,则D、O两点电势φD的为-2V,φO的为2V.