题目内容
8. 如图所示,S处有一电子源,可向纸面内任意方向发射速率为1.6×106m/s的电子,电子质量为9.1×10-31kg,电荷量为1.6×10-19C,重力忽略不计.一平板MN垂直于纸面,且在纸面内的长度为9.10cm,中点O与S间的距离为4.55cm,MN与SO直线的夹角为θ;板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度大小为2.0×10-4T.设某个电子打在板上可能位置的区域长度为l,则l可能为( )
如图所示,S处有一电子源,可向纸面内任意方向发射速率为1.6×106m/s的电子,电子质量为9.1×10-31kg,电荷量为1.6×10-19C,重力忽略不计.一平板MN垂直于纸面,且在纸面内的长度为9.10cm,中点O与S间的距离为4.55cm,MN与SO直线的夹角为θ;板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度大小为2.0×10-4T.设某个电子打在板上可能位置的区域长度为l,则l可能为( )| A. | 13.65cm | B. | 7.50cm | C. | 4.55cm | D. | 3.15cm |
分析 由洛仑兹力充当向心力可求得粒子运动半径,再由几何关系可知,电子运动的范围,由几何关系即可求出电子打在板上可能位置的区域的长度.
解答 解:由洛仑兹力充当向心力可得;Bqv=m$\frac{{v}^{2}}{R}$,
解得:R=$\frac{mv}{Bq}$=$\frac{9.1×1{0}^{-31}×1.6×1{0}^{6}}{2×1{0}^{-4}×1.6×1{0}^{-19}}$m=0.0455m=4.55cm;
所有粒子的圆心组成以S为圆心,R为半径的圆;电子出现的区域为以S为圆心,以9.1cm半径的圆形区域内,如图中大圆所示;
故当θ=90°时,纸板MN均在该区域内,故l=9.1cm;
当角度小于90°,电子打在板上的区域长度就为4.55cm;
故C正确、ABD错误.
故选:C.
点评 对于带电粒子在磁场中的运动情况分析,一般是确定圆心位置,根据几何关系求半径,结合洛伦兹力提供向心力求解未知量

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.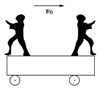 如图所示,光滑平面上有一辆质量为4m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度v0向右匀速运动.某一时刻,站在车右端的乙先以相对地面向右的速度v跳离小车,然后站在车左端的甲以相对于地面向左的速度v跳离小车.两人都离开小车后,小车的速度将是( )
如图所示,光滑平面上有一辆质量为4m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度v0向右匀速运动.某一时刻,站在车右端的乙先以相对地面向右的速度v跳离小车,然后站在车左端的甲以相对于地面向左的速度v跳离小车.两人都离开小车后,小车的速度将是( )
 如图所示,光滑平面上有一辆质量为4m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度v0向右匀速运动.某一时刻,站在车右端的乙先以相对地面向右的速度v跳离小车,然后站在车左端的甲以相对于地面向左的速度v跳离小车.两人都离开小车后,小车的速度将是( )
如图所示,光滑平面上有一辆质量为4m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度v0向右匀速运动.某一时刻,站在车右端的乙先以相对地面向右的速度v跳离小车,然后站在车左端的甲以相对于地面向左的速度v跳离小车.两人都离开小车后,小车的速度将是( )| A. | 1.5v0 | B. | v0 | ||
| C. | 大于v0,小于1.5v0 | D. | 大于1.5v0 |
13.如图所示,A和B是带电荷量为Q的等量异种电荷,距离为d.一个带电荷量为+q的电荷C在外力F的乍用下绕负电荷B做匀速圆周运动,轨道半径为$\frac{d}{2}$.取无穷远处为电势零点,电荷C运动轨迹上的P、Q两点是与AB连线垂直的直径的两个端点,忽略重力及运动电荷对电场的影响,则( )
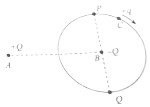

| A. | 电荷C的运动轨迹上各点的电势均为负值 | |
| B. | 电荷C顺时针运动,则从P到Q的运动过程中,电势能先增打后减小 | |
| C. | 电荷C运动一周,外力F做功为零 | |
| D. | 若电荷C绕A做同样的运动,与绕B的运动相比,在对应位置需要的外力F大小相等,方向相反 |
20. 如图所示,Q1、Q2为真空中的两等量异种点电荷,Q1带正电,Q2带负电,两点电荷的连线沿水平方向,有一根足够长的光滑绝缘杆位于两电荷连线的正上方,且与连线平行,一带负电的圆环A穿在光滑的杆上,圆环的半径略大于杆,给圆环一初速度,使其自左向右依次通过a、b、c三点,已知ab=bc,且b点位于Q1、Q2连线的中垂线上,a,c两点离电荷Q1,Q2较远,则下列说法正确的是( )
如图所示,Q1、Q2为真空中的两等量异种点电荷,Q1带正电,Q2带负电,两点电荷的连线沿水平方向,有一根足够长的光滑绝缘杆位于两电荷连线的正上方,且与连线平行,一带负电的圆环A穿在光滑的杆上,圆环的半径略大于杆,给圆环一初速度,使其自左向右依次通过a、b、c三点,已知ab=bc,且b点位于Q1、Q2连线的中垂线上,a,c两点离电荷Q1,Q2较远,则下列说法正确的是( )
 如图所示,Q1、Q2为真空中的两等量异种点电荷,Q1带正电,Q2带负电,两点电荷的连线沿水平方向,有一根足够长的光滑绝缘杆位于两电荷连线的正上方,且与连线平行,一带负电的圆环A穿在光滑的杆上,圆环的半径略大于杆,给圆环一初速度,使其自左向右依次通过a、b、c三点,已知ab=bc,且b点位于Q1、Q2连线的中垂线上,a,c两点离电荷Q1,Q2较远,则下列说法正确的是( )
如图所示,Q1、Q2为真空中的两等量异种点电荷,Q1带正电,Q2带负电,两点电荷的连线沿水平方向,有一根足够长的光滑绝缘杆位于两电荷连线的正上方,且与连线平行,一带负电的圆环A穿在光滑的杆上,圆环的半径略大于杆,给圆环一初速度,使其自左向右依次通过a、b、c三点,已知ab=bc,且b点位于Q1、Q2连线的中垂线上,a,c两点离电荷Q1,Q2较远,则下列说法正确的是( )| A. | 当圆环位于b点的左侧时,杆对环的弹力方向先是竖直向上后是竖直向下的 | |
| B. | 圆环从a运动至b的过程中,速度先增大后减小 | |
| C. | 圆环经过b点时的动能最小 | |
| D. | 圆环在a点的电势能大于在c点的电势能 |
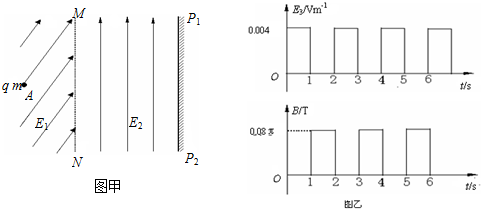
17. 如图甲所示,直线AB是某电场中的一条电场线,若在A点放置一初速度为零的质子,质子仅在电场力作用下,沿直线AB由A运动到B过程中速度随时间变化的图象如图乙所示.则下列说法中正确的是( )
如图甲所示,直线AB是某电场中的一条电场线,若在A点放置一初速度为零的质子,质子仅在电场力作用下,沿直线AB由A运动到B过程中速度随时间变化的图象如图乙所示.则下列说法中正确的是( )
 如图甲所示,直线AB是某电场中的一条电场线,若在A点放置一初速度为零的质子,质子仅在电场力作用下,沿直线AB由A运动到B过程中速度随时间变化的图象如图乙所示.则下列说法中正确的是( )
如图甲所示,直线AB是某电场中的一条电场线,若在A点放置一初速度为零的质子,质子仅在电场力作用下,沿直线AB由A运动到B过程中速度随时间变化的图象如图乙所示.则下列说法中正确的是( )| A. | A点的电场强度一定大于B点的电场强度 | |
| B. | 电场一定不是孤立点电荷电场 | |
| C. | 质子从A到B的过程中,在连续相等的时间间隔内,电场力做功的平均功率一定相等 | |
| D. | 质子从A到B的过程中,在连续相等的时间间隔内,电场力的冲量一定相等 |
18.关于曲线运动,下列说法中正确的是( )
| A. | 物体做曲线运动时,有可能处于平衡状态 | |
| B. | 做曲线运动的物体,速度可能不变 | |
| C. | 所有做曲线运动的物体,速度一定发生改变 | |
| D. | 所有做曲线运动的物体,加速度方向与速度方向始终一致 |
 如图所示,光滑水平面上放置质量分别为m甲=2kg、m乙=3kg的甲、乙两辆小车,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离),甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.5.一根通过细线拴着且被压缩的轻质弹簧固定在甲车的左端,质量为m=1kg的滑块P(可视为质点)与弹簧的右端接触但不相连,此时弹簧的弹性势能Ep=15J,弹簧原长小于甲车长度,整个系统处于静止状态,现剪断细线,求:
如图所示,光滑水平面上放置质量分别为m甲=2kg、m乙=3kg的甲、乙两辆小车,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离),甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.5.一根通过细线拴着且被压缩的轻质弹簧固定在甲车的左端,质量为m=1kg的滑块P(可视为质点)与弹簧的右端接触但不相连,此时弹簧的弹性势能Ep=15J,弹簧原长小于甲车长度,整个系统处于静止状态,现剪断细线,求: