题目内容
18. 如图所示,光滑水平面上放置质量分别为m甲=2kg、m乙=3kg的甲、乙两辆小车,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离),甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.5.一根通过细线拴着且被压缩的轻质弹簧固定在甲车的左端,质量为m=1kg的滑块P(可视为质点)与弹簧的右端接触但不相连,此时弹簧的弹性势能Ep=15J,弹簧原长小于甲车长度,整个系统处于静止状态,现剪断细线,求:
如图所示,光滑水平面上放置质量分别为m甲=2kg、m乙=3kg的甲、乙两辆小车,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离),甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.5.一根通过细线拴着且被压缩的轻质弹簧固定在甲车的左端,质量为m=1kg的滑块P(可视为质点)与弹簧的右端接触但不相连,此时弹簧的弹性势能Ep=15J,弹簧原长小于甲车长度,整个系统处于静止状态,现剪断细线,求:(1)滑块P滑离甲车时的瞬时速度大小;
(2)滑块P滑上乙车后最终未滑离乙车,滑块P在乙车上滑行的距离.(取g=10m/s2)
分析 (1)滑块P在甲车滑行的过程,根据动量守恒定律和机械能守恒定律结合求解滑块P滑离甲车时的瞬时速度大小;
(2)对P和乙车组成的系统,运用动量守恒定律求出滑块P和乙车最终的共同速度,再由能量守恒定律求滑块P在乙车上滑行的距离.
解答 解:(1)设滑块P滑离甲车时的瞬时速度大小为vp,甲车和乙车的速率为v甲.
在弹簧弹开物块P的过程中,规定向右为正方向,对P、甲、乙两车组成的系统,由动量守恒定律得:
0=mvP-(m甲+m乙)v甲,
由P、甲、乙两车组成的系统机械能守恒得
Ep=$\frac{1}{2}$mvP2+$\frac{1}{2}$(m甲+m乙)v甲2,
解得 v甲=1m/s,vp=5m/s
(2)滑块P在乙车上滑动的过程中,P与乙组成的系统动量守恒,规定向右为正方向,根据动量守恒定律得:
mvP-m乙v甲=(m乙+m)v
滑块P与乙车系统能量守恒,得 μmgs=$\frac{1}{2}$mvP2+$\frac{1}{2}$m乙v甲2-$\frac{1}{2}$(m乙+m)v2.
解得,滑块P在乙车上滑行的距离 s=2.7m
答:
(1)滑块P滑离甲车时的瞬时速度大小是5m/s;
(2)滑块P滑上乙车后最终未滑离乙车,滑块P在乙车上滑行的距离是2.7m.
点评 本题考查了动量守恒定律和能量守恒定律的运用,关键灵活地选择研究的系统,明确研究的过程,要知道摩擦生热与相对位移有关.

练习册系列答案
相关题目
9.通过观测冥王星的卫星,可以推算出冥王星的质量.假设卫星绕冥王星做匀速圆周运动,除了引力常量外,至少还需要两个物理量才能计算出冥王星的质量.这两个物理量可以是( )
| A. | 卫星的质量和轨道半径 | B. | 卫星的速度和角速度 | ||
| C. | 卫星的质量和角速度 | D. | 卫星的运行周期和轨道半径 |
6.一质点在某段时间内做曲线运动,则在这段时间内( )
| A. | 速度一定在不断地改变,加速度可以不变 | |
| B. | 速度一定在不断地改变,加速度也一定在不断地改变 | |
| C. | 速度一定在不断地改变,加速度也可以在不断地改变 | |
| D. | 速度可以不变,加速度也一定在不断地改变 |
13.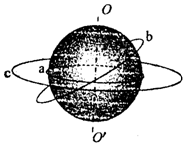 如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径近似等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是( )
如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径近似等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是( )
 如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径近似等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是( )
如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径近似等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是( )| A. | a、b、c的角速度大小关系为ωa=ωb>ωc | |
| B. | a、b、c的向心加速度大小关系为ab>ac>aa | |
| C. | a、b、c的线速度大小关系为va=vb>vc | |
| D. | a、b、c的周期关系为Ta=Tc<Tb |
7.下列说法正确的是( )
| A. | 氢原子的发射光谱是连续光谱 | |
| B. | 比结合能越小表示原子核中的核子结合得越牢固 | |
| C. | 光子具有波粒二象性,其他的微观粒子不具有波粒二象性 | |
| D. | 氢核、中子和氘核的质量分别为m1、m2、m3,当氢核与中子结合为氘核时,放出的能量为(m1+m2-m3)c2 |
 如图所示,圆形区域内存在垂直于圆面向里的匀强磁场,磁感应强度大小为B.A、C、D三点在圆上,O为圆心,且AD=AC=$\sqrt{3}$AO.带电粒子a从A点沿AO方向射入磁场,从D点离开磁场区域;带电粒子b从A点沿AO方向射入磁场,从C点离开磁场区域.已知粒子a的质量为m、电荷量为q(q>0),粒子a、b带等量异种电荷,且粒子b从A点射入磁场时的动能是粒子a从A点射入磁场时动能的2倍,不计粒子重力,求:
如图所示,圆形区域内存在垂直于圆面向里的匀强磁场,磁感应强度大小为B.A、C、D三点在圆上,O为圆心,且AD=AC=$\sqrt{3}$AO.带电粒子a从A点沿AO方向射入磁场,从D点离开磁场区域;带电粒子b从A点沿AO方向射入磁场,从C点离开磁场区域.已知粒子a的质量为m、电荷量为q(q>0),粒子a、b带等量异种电荷,且粒子b从A点射入磁场时的动能是粒子a从A点射入磁场时动能的2倍,不计粒子重力,求:

 如图所示,S处有一电子源,可向纸面内任意方向发射速率为1.6×106m/s的电子,电子质量为9.1×10-31kg,电荷量为1.6×10-19C,重力忽略不计.一平板MN垂直于纸面,且在纸面内的长度为9.10cm,中点O与S间的距离为4.55cm,MN与SO直线的夹角为θ;板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度大小为2.0×10-4T.设某个电子打在板上可能位置的区域长度为l,则l可能为( )
如图所示,S处有一电子源,可向纸面内任意方向发射速率为1.6×106m/s的电子,电子质量为9.1×10-31kg,电荷量为1.6×10-19C,重力忽略不计.一平板MN垂直于纸面,且在纸面内的长度为9.10cm,中点O与S间的距离为4.55cm,MN与SO直线的夹角为θ;板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度大小为2.0×10-4T.设某个电子打在板上可能位置的区域长度为l,则l可能为( )