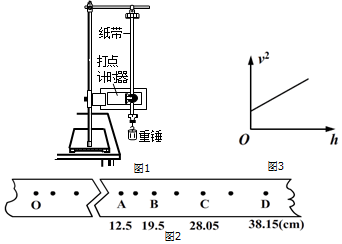
题目内容
3.如图甲所示,在边界MN左侧存在与竖直方向成37°的匀强电场E1=0.5N/C,在MN的右侧有竖直向上的匀强电场E2,还有垂直纸面向内的匀强磁场B(图甲中未画出)和水平向右的匀强电场E3(图甲中未画出),B和E3随时间变化的情况如图乙所示,P1P2为距MN边界2.295m的竖直墙壁,现有一带正电微粒质量为4×10-7kg,电量为1×10-5C,从左侧电场中距MN边界L处的A处无初速释放后,沿直线以1m/s速度垂直MN边界进入右侧场区,设此时刻t=0,取g=10m/s2.求: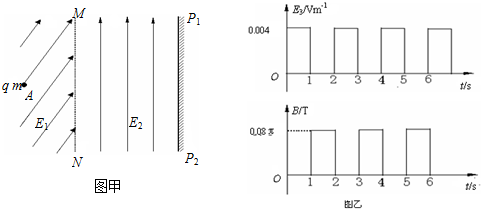
(1)A点距MN边界的距离L多大(sin37°=0.6);
(2)进入右侧场区1s内带电微粒仍垂直MN边界运动,则E2多大;
(3)在(2)问的条件下,带电微粒在MN右侧场区中运动了1.5s时的速度;
(4)在(2)问的条件下,带电微粒在MN右侧场区中运动多长时间与墙壁碰撞?($\frac{1.2}{2π}$≈0.19)
分析 (1)微粒从A处无初速释放后,沿直线垂直MN边界进入右侧场区,可知合力的方向与MN垂直,抓住竖直方向上平衡,水平方向上产生加速度,结合速度位移公式求出A点距离MN边界的距离.
(2)进入右侧场区1s内带电微粒仍垂直MN边界运动,可知微粒所受的重力和竖直方向上的电场力平衡,结合平衡求出电场强度E2的大小.
(3)粒子在前1s内做匀加速最小运动,根据牛顿第二定律和速度时间公式求出1s末的速度,1s-1.5s内,带电粒子在复合场中做匀速圆周运动,根据带电粒了在磁场中的运动规律明确转动时间,则可确定其速度方向;
(4)根据带电粒子在右侧混合场中的运动情况,明确粒子何时才能与墙壁相碰撞.
解答 解:(1)设MN左侧匀强电场场强为E1,方向与水平方向夹角为θ,
沿水平方向有 qE1cosθ=ma
沿竖直方向有 qE1sinθ=mg
对水平方向的匀加速运动有:v2=2aL
代入数据可解得L=$\frac{1}{15}$m.
(2)由于带电微粒进入右侧场区后仍垂直MN运动,有qE2=mg
代入数据可解得 E2=0.4N/C
(3)带电微粒在MN右侧场区始终满足 qE2=mg
在0~1s时间内,带电微粒在E3电场中 a=$\frac{q{E}_{3}}{m}=\frac{1×1{0}^{-5}×0.004}{4×1{0}^{-7}}m/{s}^{2}=0.1m/{s}^{2}$.
带电微粒在1s时的速度大小为 v1=v+at=1+0.1×1=1.1m/s,
在1~1.5s时间内,带电微粒在磁场B中运动,周期T=$\frac{2πm}{qB}=\frac{2π×4×1{0}^{-7}}{1×1{0}^{-5}×0.08π}=1s$,
在1~1.5s时间内,带电微粒在磁场B中正好作半个圆周运动.所以带电微粒在MN右侧场区中运动了1.5s时的速度大小为1.1m/s,方向水平向左.
(4)在0s~1s时间内带电微粒前进距离 s1=vt+$\frac{1}{2}$at2=1×1+$\frac{1}{2}$×0.1×12=1.05m.
带电微粒在磁场B中作圆周运动的半径r=$\frac{mv}{qB}=\frac{4×1{0}^{-7}×1.1}{1×1{0}^{-5}×0.08π}$=$\frac{1.1}{2π}m$.
因为r+s1<2.28m,所以在1s~2s时间内带电微粒未碰及墙壁.
在2s~3s时间内带电微粒作匀加速运动,加速度仍为 a=0.1m/s2,
在3s内带电微粒共前进距离
s3=$v{t}_{3}+\frac{1}{2}a{{t}_{3}}^{2}=1×2+\frac{1}{2}×0.1×{2}^{2}$m=2.2m.
在3s时带电微粒的速度大小为v3=v+at3=1+0.1×2m/s=1.2m/s.
在3s~4s时间内带电微粒在磁场B中作圆周运动的半径${r}_{3}=\frac{m{v}_{3}}{qB}=\frac{4×1{0}^{-7}×1.2}{1×1{0}^{-5}×0.08π}=\frac{1.2}{2π}$=0.19m,
因为r3+s3>2.295m,所以在4s时间内带电微粒碰及墙壁
带电微粒在3s以后运动情况如右图,其中 d=2.295-2.2=0.095m,
sinθ=$\frac{d}{{r}_{3}}=0.5$,θ=30° 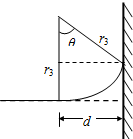
所以,带电微粒作圆周运动的时间为${t}_{3}=\frac{{T}_{3}}{12}=\frac{2πm}{12qB}=\frac{2π×4×1{0}^{-7}}{12×1×1{0}^{-5}×0.08π}$=$\frac{1}{12}$s.
带电微粒与墙壁碰撞的时间为 t总=3+$\frac{1}{12}$=$\frac{37}{12}$s.
答:(1)A点距MN边界的距离L为$\frac{1}{15}m$;
(2)进入右侧场区1s内带电微粒仍垂直MN边界运动,则E2为0.4N/C;
(3)带电微粒在MN右侧场区中运动了1.5s时的速度为1.1m/s,方向水平向左;
(4)带电微粒在MN右侧场区中运动$\frac{37}{12}$s与墙壁碰撞.
点评 本题考查带电粒子在复合场中的运动,要注意能正确分析带电物体的运动情况及运动情况,结合带电粒子在电场和磁场中的运动规律灵活选择物理规律求解.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案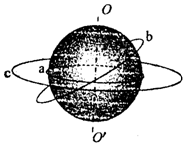 如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径近似等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是( )
如图所示,a为放在赤道上相对地球静止的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星(轨道半径近似等于地球半径),c为地球的同步卫星,以下关于a、b、c的说法中正确的是( )| A. | a、b、c的角速度大小关系为ωa=ωb>ωc | |
| B. | a、b、c的向心加速度大小关系为ab>ac>aa | |
| C. | a、b、c的线速度大小关系为va=vb>vc | |
| D. | a、b、c的周期关系为Ta=Tc<Tb |
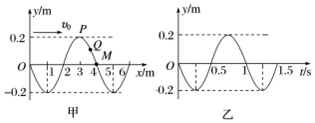
| A. | 该简谐横波的传播速度为4 m/s | |
| B. | 从此时刻起,经过2s,P质点运动了8m的路程 | |
| C. | 从此时刻起,P质点比Q质点先回到平衡位置 | |
| D. | 图乙可能是图甲x=4 m处质点的振动图象 |
 如图所示,B、C、D、E、F五个球并排放置在光滑的水平面上,B、C、D、E四球质量相等,而F球质量小于B球质量,A球的质量等于F球质量,A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )
如图所示,B、C、D、E、F五个球并排放置在光滑的水平面上,B、C、D、E四球质量相等,而F球质量小于B球质量,A球的质量等于F球质量,A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )| A. | 五个小球静止,一个小球运动 | B. | 四个小球静止,两个小球运动 | ||
| C. | 三个小球静止,三个小球运动 | D. | 六个小球都运动 |
 如图所示,S处有一电子源,可向纸面内任意方向发射速率为1.6×106m/s的电子,电子质量为9.1×10-31kg,电荷量为1.6×10-19C,重力忽略不计.一平板MN垂直于纸面,且在纸面内的长度为9.10cm,中点O与S间的距离为4.55cm,MN与SO直线的夹角为θ;板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度大小为2.0×10-4T.设某个电子打在板上可能位置的区域长度为l,则l可能为( )
如图所示,S处有一电子源,可向纸面内任意方向发射速率为1.6×106m/s的电子,电子质量为9.1×10-31kg,电荷量为1.6×10-19C,重力忽略不计.一平板MN垂直于纸面,且在纸面内的长度为9.10cm,中点O与S间的距离为4.55cm,MN与SO直线的夹角为θ;板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度大小为2.0×10-4T.设某个电子打在板上可能位置的区域长度为l,则l可能为( )| A. | 13.65cm | B. | 7.50cm | C. | 4.55cm | D. | 3.15cm |
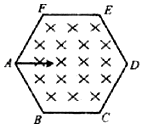 如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂离子纸面向里的匀强磁场.三个带正电的粒子以相同的速度υ先后从A点沿AD方向射入匀强磁场区域.粒子在运动过程中只受磁场力作用,已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上的某一点垂 直边界飞出磁场区域.则下列说法正确的是( )
如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂离子纸面向里的匀强磁场.三个带正电的粒子以相同的速度υ先后从A点沿AD方向射入匀强磁场区域.粒子在运动过程中只受磁场力作用,已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上的某一点垂 直边界飞出磁场区域.则下列说法正确的是( )| A. | 编号为①的粒子的比荷为$\frac{{\sqrt{3}υ}}{Ba}$ | |
| B. | 编号为②的粒子在磁场区域内运动的时间$t=\frac{πm}{6qB}$ | |
| C. | 编号为③的粒子在ED边上飞出的位置与E点的距离(2$\sqrt{3}$-3)a | |
| D. | 三个粒子在磁场内运动的时间依次减少并且为4:2:1 |
 如图所示,质量为1kg的物体(可视为质点)在水平传送带上被传送,A为终端皮带轮,传送带与皮带轮之间不打滑且与皮带在C点相切,物体刚放上皮带时的速度为0,距C点的距离为1m,皮带轮的半径为10cm,重力加速度g=10m/s2,若皮带轮转动的线速度大小为1m/s,物体运动到C点的前速度已达到1m/s,则( )
如图所示,质量为1kg的物体(可视为质点)在水平传送带上被传送,A为终端皮带轮,传送带与皮带轮之间不打滑且与皮带在C点相切,物体刚放上皮带时的速度为0,距C点的距离为1m,皮带轮的半径为10cm,重力加速度g=10m/s2,若皮带轮转动的线速度大小为1m/s,物体运动到C点的前速度已达到1m/s,则( )| A. | 物体在C点对传送带的压力大小为10N | |
| B. | 物体与传送带间的摩擦因数至少为0.1 | |
| C. | 物体到达C点后将沿皮带下滑一段距离再离开皮带 | |
| D. | 物体与传送带摩擦产生的热量为0.5J |