题目内容
14. 如图所示,粗细均匀竖直放置的玻璃管中,P为一小活塞,有一段水银柱将封闭在玻璃管中的空气分成上、下两部分,活塞和水银柱都静止不动.现在用力向下压活塞,使得活塞向下移动一段距离L,同时水银柱将向下缓慢移动一段距离为H,其中温度不变,则有( )
如图所示,粗细均匀竖直放置的玻璃管中,P为一小活塞,有一段水银柱将封闭在玻璃管中的空气分成上、下两部分,活塞和水银柱都静止不动.现在用力向下压活塞,使得活塞向下移动一段距离L,同时水银柱将向下缓慢移动一段距离为H,其中温度不变,则有( )| A. | L>H | B. | L<H | C. | L=H | D. | 无法判断 |
分析 向下压活塞过程气体温度不变,气体发生等温变化,应用玻意耳定律求出气体体积的变化量,由图示求出两部分气体的压强关系,然后判断两部分气体体积变化关系大小,然后判断L与H的大小关系.
解答 解:向下压活塞时气体的压强增大,两部分气体的压强增加量△p相等,
气体发生等温变化,由玻意耳定律得:pV=p′V′,△V=V-V′=$\frac{△p}{p′}$V,
由图示可知,pB=pA+h>pA,pB′=pA′+h>pA′,
由于B的压强pB′大于A的压强pA′,则△VA>△VB,则L>H;
故选:A.
点评 本题考查了比较L与H大小关系,分析清楚图示情景,知道两部分气体压强关系是解题的关键,应用玻意耳定律可以解题.

练习册系列答案
相关题目
17. 倾角为θ的足够长的粗糙斜面放置于粗糙水平地面上,重力为mg的物块与斜面之间的动摩擦因数为μ.若该物块以某一初速度滑上斜面,则经过一段时间后回到斜面底端,此过程中斜面保持静止.现将该物块再次置于斜面上,同时对物体施加一平行于斜面向上的外力F(F=mgsinθ-μmgcosθ),使物块在斜面上恰好不下滑,然后逐渐增大F.已知各个接触面之间的最大静摩擦力等于滑动摩擦力,在F逐渐增大的过程中,下列说法正确的是( )
倾角为θ的足够长的粗糙斜面放置于粗糙水平地面上,重力为mg的物块与斜面之间的动摩擦因数为μ.若该物块以某一初速度滑上斜面,则经过一段时间后回到斜面底端,此过程中斜面保持静止.现将该物块再次置于斜面上,同时对物体施加一平行于斜面向上的外力F(F=mgsinθ-μmgcosθ),使物块在斜面上恰好不下滑,然后逐渐增大F.已知各个接触面之间的最大静摩擦力等于滑动摩擦力,在F逐渐增大的过程中,下列说法正确的是( )
 倾角为θ的足够长的粗糙斜面放置于粗糙水平地面上,重力为mg的物块与斜面之间的动摩擦因数为μ.若该物块以某一初速度滑上斜面,则经过一段时间后回到斜面底端,此过程中斜面保持静止.现将该物块再次置于斜面上,同时对物体施加一平行于斜面向上的外力F(F=mgsinθ-μmgcosθ),使物块在斜面上恰好不下滑,然后逐渐增大F.已知各个接触面之间的最大静摩擦力等于滑动摩擦力,在F逐渐增大的过程中,下列说法正确的是( )
倾角为θ的足够长的粗糙斜面放置于粗糙水平地面上,重力为mg的物块与斜面之间的动摩擦因数为μ.若该物块以某一初速度滑上斜面,则经过一段时间后回到斜面底端,此过程中斜面保持静止.现将该物块再次置于斜面上,同时对物体施加一平行于斜面向上的外力F(F=mgsinθ-μmgcosθ),使物块在斜面上恰好不下滑,然后逐渐增大F.已知各个接触面之间的最大静摩擦力等于滑动摩擦力,在F逐渐增大的过程中,下列说法正确的是( )| A. | 物块受到的摩擦力先减小后增大,最后保持不变 | |
| B. | 地面对斜面的支持力一直减小 | |
| C. | 地面对斜面的摩擦力一直增大 | |
| D. | 斜面一定不会滑动 |
2. 如图所示,长为2L的轻质杆两端固定质量分别为m和2m的两小球P、Q,杆可绕中点的轴O在竖直平面内无摩擦转动.若给静止于最高点的P球一初速度,使P、Q两球在竖直面内做圆周运动.不计空气阻力,重力加速度为g,下列说法正确的是( )
如图所示,长为2L的轻质杆两端固定质量分别为m和2m的两小球P、Q,杆可绕中点的轴O在竖直平面内无摩擦转动.若给静止于最高点的P球一初速度,使P、Q两球在竖直面内做圆周运动.不计空气阻力,重力加速度为g,下列说法正确的是( )
 如图所示,长为2L的轻质杆两端固定质量分别为m和2m的两小球P、Q,杆可绕中点的轴O在竖直平面内无摩擦转动.若给静止于最高点的P球一初速度,使P、Q两球在竖直面内做圆周运动.不计空气阻力,重力加速度为g,下列说法正确的是( )
如图所示,长为2L的轻质杆两端固定质量分别为m和2m的两小球P、Q,杆可绕中点的轴O在竖直平面内无摩擦转动.若给静止于最高点的P球一初速度,使P、Q两球在竖直面内做圆周运动.不计空气阻力,重力加速度为g,下列说法正确的是( )| A. | Q球在运动过程中机械能守恒 | |
| B. | P从最高点运动到最低点过程中杆对其做功为2mgL | |
| C. | Q到达最高点时杆对其作用力的最小值大小为2mg | |
| D. | 为使P、Q两球能够做圆周运动,P球的初速度不能小于2$\sqrt{gL}$ |
9. 如图所示,竖直平面内有一光滑直杆AB,杆与水平方向的夹角为θ(0°≤θ≤90°),一质量为m的小圆环套在直杆上,给小圆环施加一与该竖直平面平行的恒力F,并从A端由静止释放,改变直杆和水平方向的夹角θ,当直杆与水平方向的夹角为30°时,小圆环在直杆上运动的时间最短,重力加速度为g,则( )
如图所示,竖直平面内有一光滑直杆AB,杆与水平方向的夹角为θ(0°≤θ≤90°),一质量为m的小圆环套在直杆上,给小圆环施加一与该竖直平面平行的恒力F,并从A端由静止释放,改变直杆和水平方向的夹角θ,当直杆与水平方向的夹角为30°时,小圆环在直杆上运动的时间最短,重力加速度为g,则( )
 如图所示,竖直平面内有一光滑直杆AB,杆与水平方向的夹角为θ(0°≤θ≤90°),一质量为m的小圆环套在直杆上,给小圆环施加一与该竖直平面平行的恒力F,并从A端由静止释放,改变直杆和水平方向的夹角θ,当直杆与水平方向的夹角为30°时,小圆环在直杆上运动的时间最短,重力加速度为g,则( )
如图所示,竖直平面内有一光滑直杆AB,杆与水平方向的夹角为θ(0°≤θ≤90°),一质量为m的小圆环套在直杆上,给小圆环施加一与该竖直平面平行的恒力F,并从A端由静止释放,改变直杆和水平方向的夹角θ,当直杆与水平方向的夹角为30°时,小圆环在直杆上运动的时间最短,重力加速度为g,则( )| A. | 恒力F一定沿与水平方向夹30°斜向右下的方向 | |
| B. | 恒力F和小圆环的重力的合力一定沿与水平方向夹30°斜向右下的方向 | |
| C. | 若恒力F的方向水平向右,则恒力F的大小为$\sqrt{3}$mg | |
| D. | 恒力F的最小值为$\frac{\sqrt{3}}{2}$mg |
 如图所示,竖直平面内的轨道是由倾角为θ的粗糙直轨道AB和半径为R的光滑圆弧轨道BCD相切于B点而构成的,E为轨道的最低点.质量为m的小物块(可视为质点)从直轨道上的P点由静止释放,物块沿轨道向下运动.物块与轨道AB间的动摩擦因数为μ.
如图所示,竖直平面内的轨道是由倾角为θ的粗糙直轨道AB和半径为R的光滑圆弧轨道BCD相切于B点而构成的,E为轨道的最低点.质量为m的小物块(可视为质点)从直轨道上的P点由静止释放,物块沿轨道向下运动.物块与轨道AB间的动摩擦因数为μ. 一种报警装置原理如图,未知外力时,气缸内密闭空气柱(可视为理想气体)长度为l,温度为T,不计活塞和气缸之间的摩擦.若气缸内温度不变,在外力作用下当活塞下降距离h时,气缸内压强达到临界值,传感器将报警.若保持空气柱长度l不变,气缸内温度升至T1时,传感器也将报警,求T1.
一种报警装置原理如图,未知外力时,气缸内密闭空气柱(可视为理想气体)长度为l,温度为T,不计活塞和气缸之间的摩擦.若气缸内温度不变,在外力作用下当活塞下降距离h时,气缸内压强达到临界值,传感器将报警.若保持空气柱长度l不变,气缸内温度升至T1时,传感器也将报警,求T1. 图中的竖直圆筒固定不动,粗筒横截面积是细筒的4倍,细筒足够长.粗筒中A、B两轻质活塞间封有空气,气柱长l=20cm.活塞A上方的水银深H=10cm,两活塞与筒壁间的摩擦不计.大气压强p0=75cmHg.用外力F竖直向上托住活塞B,使之处于静止状态.水银面与粗筒上端相平.现缓慢升高温度,直至水银的一半进入细筒中,求:
图中的竖直圆筒固定不动,粗筒横截面积是细筒的4倍,细筒足够长.粗筒中A、B两轻质活塞间封有空气,气柱长l=20cm.活塞A上方的水银深H=10cm,两活塞与筒壁间的摩擦不计.大气压强p0=75cmHg.用外力F竖直向上托住活塞B,使之处于静止状态.水银面与粗筒上端相平.现缓慢升高温度,直至水银的一半进入细筒中,求:



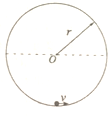 如图所示,宇航员在地球表面完成以下实验:在固定的竖直光滑圆弧轨道内部的最低点,给质量为m的小球水平初速度v,小球恰能在竖直平面内做完整的圆周运动,而宇航员在某星球表面重复上述实验时发现小球只能上升至圆心等高处.已知该星球半径为地球半径的2倍,小球可视为质点,可求得该星球和地球的密度之比为( )
如图所示,宇航员在地球表面完成以下实验:在固定的竖直光滑圆弧轨道内部的最低点,给质量为m的小球水平初速度v,小球恰能在竖直平面内做完整的圆周运动,而宇航员在某星球表面重复上述实验时发现小球只能上升至圆心等高处.已知该星球半径为地球半径的2倍,小球可视为质点,可求得该星球和地球的密度之比为( )