已知函数f（x）=a•2^|x|+1（a≠0），定义函数给出下列命题：

①F（x）=|f（x）|；

②函数F（x）是奇函数；

③当a＜0时，若mn＜0，m+n＞0，总有F（m）+F（n）＜0成立，

其中所有正确命题的序号是（　　）

已知函数f（x）=x﹣[x]，其中[x]表示不超过实数x的最大整数．若关于x的方程f（x）=kx+k有三个不同的实根，则实数k的取值范围是（　　）

双曲线C的左右焦点分别为F₁，F₂，且F₂恰为抛物线y²=4x的焦点，设双曲线C与该抛物线的一个交点为A，若△AF₁F₂是以AF₁为底边的等腰三角形，则双曲线C的离心率为（　　）

已知{a_n}为等差数列，a₁+a₃+a₅=105，a₂+a₄+a₆=99，以S_n表示{a_n}的前n项和，则使得S_n达到最大值的n是（　　）

设变量x，y满足约束条件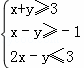，则目标函数的取值范围是（　　）

设函数f（x），g（x）在[a，b]上均可导，且f′（x）＜g′（x），则当a＜x＜b时，有（　　）

设曲线y=ax²在点（1，a）处的切线与直线2x﹣y﹣6=0平行，则a=（　　）

定义在R上的偶函数f（x），在（0，+∞）上是增函数，则（　　）

i是虚数单位，计算i+i²+i³=（　　）

x²﹣3x+2≠0是x≠1的（　　）