题目内容
已知函数f(x)=a•2|x|+1(a≠0),定义函数![]() 给出下列命题:
给出下列命题:
①F(x)=|f(x)|;
②函数F(x)是奇函数;
③当a<0时,若mn<0,m+n>0,总有F(m)+F(n)<0成立,
其中所有正确命题的序号是( )
|
| A. | ② | B. | ①③ | C. | ②③ | D. | ①② |
解答:
解:由题意得,F(x)=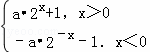 ,
,
而|f(x)|=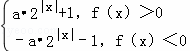 ,它和F(x)并不是同一个函数,故①错误;
,它和F(x)并不是同一个函数,故①错误;
∵函数f(x)=a•2|x|+1是偶函数,
当x>0时,﹣x<0,则F(﹣x)=﹣f(﹣x)=﹣f(x)=﹣F(x);
当x<0时,﹣x>0,则F(﹣x)=f(﹣x)=f(x)=﹣F(x);
故函数F(x)是奇函数,②正确;
当a<0时,F(x)在(0,+∞)上是减函数,
若mn<0,m+n>0,总有m>﹣n>0,
∴F(m)<F(﹣n),即f(m)<﹣F(n),
∴F(m)+F(n)<0成立,故③正确.
故选C.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目