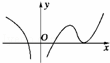
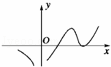
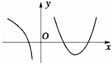
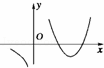
设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )
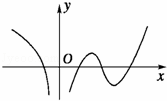
|
| A. |
| B. |
| C. |
| D. |
|
若a>0,b>0,且函数f(x)=4x3﹣ax2﹣2bx+2在x=1处有极值,则ab的最大值等于( )
|
| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
设f(x)=xlnx,若f′(x0)=2,则x0=( )
|
| A. | e2 | B. | e | C. |
| D. | ln2 |
在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x﹣2)<0的实数x的取值范围为( )
|
| A. | (0,2) | B. | (﹣2,1) | C. | (﹣∞,﹣2)∪(1,+∞) | D. | (﹣1,2) |
关于x的不等式|x﹣3|+|x﹣5|<a的解集不是空集,则a的取值范围是( )
|
| A. | a<2 | B. | a≤2 | C. | a>2 | D. | a≥2 |
曲线y=x3﹣2x+1在点(1,0)处的切线方程为( )
|
| A. | y=x﹣1 | B. | y=﹣x+1 | C. | y=2x﹣2 | D. | y=﹣2x+2 |
已知f(x)=x2+2x•f′(1),则 f′(0)等于( )
|
| A. | ﹣2 | B. | 2 | C. | 1 | D. | ﹣4 |
已知a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的( )
|
| A. | 充分而不必要条件 | B. | 必要而不充分条件 |
|
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |