题目内容
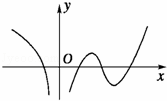
设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )
|
| A. |
| B. |
| C. |
| D. |
|
考点:
函数的图象.
专题:
应用题.
分析:
根据函数与导数的关系:可知,当f′(x)≥0时,函数f(x)单调递增;当f′(x)<0时,函数f(x)单调递减,结合函数y=f(x)的图象,利用排除法即可求解
解答:
解:根据函数与导数的关系:可知,当f′(x)≥0时,函数f(x)单调递增;当f′(x)<0时,函数f(x)单调递减
结合函数dy=f(x)的图象可知,当x<0时,函数f(x)单调递减,则f′(x)<0,排除选项A,C
当x>0时,函数f(x)先单调递增,则f′(x)≥0,排除选项B
故选D
点评:
本题主要考查了利用函数与函数的导数的关系判断函数的图象,属于基础试题

练习册系列答案
相关题目
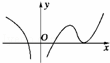
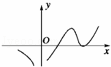
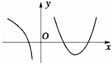
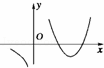
 (2008•宝坻区一模)设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )
(2008•宝坻区一模)设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( ) 设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )
设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )



 设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )
设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )



 设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )
设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )



 设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )
设f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是( )


