对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义f″(x)是y=f(x)的导函数y=f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有的同学发现“任何三次函数都有‘拐点’;任何三次函数都有对称中心;且对称中心就是‘拐点’”.请你根据这一发现判断下列命题:
(1)任意三次函数都关于点![]() 对称;
对称;
(2)存在三次函数,f'(x)=0有实数解x0,(x0,f(x0))点为函数y=f(x)的对称中心;
(3)存在三次函数有两个及两个以上的对称中心;
(4)若函数![]() ,则
,则![]()
其中正确命题的序号为( )
|
| A. | (1)(2)(4) | B. | (1)(2)(3)(4) | C. | (1)(2)(3) | D. | (2)(3) |
设p:f(x)=lnx+2x2+mx+1在(0,+∞)内单调递增,q:m≥﹣5,则p是q的( )
|
| A. | 充分不必要条件 | B. | 必要不充分条件 |
|
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
设函数f(x)=x3﹣4x+a,0<a<2.若f(x)的三个零点为x1,x2,x3,且x1<x2<x3,则( )
|
| A. | x1>﹣1 | B. | x2<0 | C. | x2>0 | D. | x3>2 |
定义运算![]() ,则符合条件
,则符合条件![]() 的复数z为( )
的复数z为( )
|
| A. | 3﹣i | B. | 1+3i | C. | 3+i | D. | 1﹣3i |
用火柴棒摆“金鱼”,如图所示:按照上面的规律,第n个“金鱼”图需要火柴棒的根数为( )
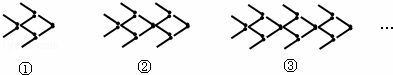
|
| A. | 6n﹣2 | B. | 8n﹣2 | C. | 6n+2 | D. | 8n+2 |
用反证法证明命题“三角形的内角至多有一个钝角”时,假设正确的是( )
|
| A. | 假设至少有一个钝角 |
|
| B. | 假设没有一个钝角 |
|
| C. | 假设至少有两个钝角 |
|
| D. | 假设没有一个钝角或至少有两个钝角 |
下列求导数运算正确的是( )
|
| A. |
| B. | (x2cosx)′=﹣2xsinx |
|
| C. |
| D. | (2sin2x)′=2cos2x |
若函数![]() 在x0处的导数等于0,那么x0等于( )
在x0处的导数等于0,那么x0等于( )
|
| A. | m | B. | ﹣m | C. | ±m | D. | m2 |
i是虚数单位.已知![]() ,则复数Z对应点落在( )
,则复数Z对应点落在( )
|
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |