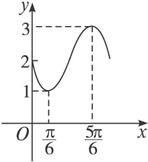
设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是( )
A.y=12+3sin![]() t,t∈[0,24]
t,t∈[0,24]
B.y=12+3sin(![]() t+π),t∈[0,24]
t+π),t∈[0,24]
C.y=12+3sin![]() t,t∈[0,24]
t,t∈[0,24]
D.y=12+3sin(![]() t+
t+![]() ),t∈[0,24]
),t∈[0,24]
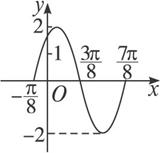
函数y=Asin(ωx+φ)(ω>0,|φ|<![]() ,x∈R)的部分图象如图所示,则函数表达式为( )
,x∈R)的部分图象如图所示,则函数表达式为( )

A.y=-4sin(![]() x+
x+![]() ) B.y=4sin(
) B.y=4sin(![]() x-
x-![]() )
)
C.y=-4sin(![]() x-
x-![]() ) D.y=4sin(
) D.y=4sin(![]() x+
x+![]() )
)
已知某海滨浴场的海浪高度f(t)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t).下表是某日各时的浪高数据.
0 55288 55296 55302 55306 55312 55314 55318 55324 55326 55332 55338 55342 55344 55348 55354 55356 55362 55366 55368 55372 55374 55378 55380 55382 55383 55384 55386 55387 55388 55390 55392 55396 55398 55402 55404 55408 55414 55416 55422 55426 55428 55432 55438 55444 55446 55452 55456 55458 55464 55468 55474 55482 266669
t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 4 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1 | 0.5 | 0.99 | 1.5 |
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T,振幅A及函数表达式.
(2)依据规定,当海浪高度高于