函数f(x)=
ax3+ax2+x+3有极值的充要条件是( )
| 1 |
| 3 |
| A、a>1或a≤0 |
| B、a>1 |
| C、0<a<1 |
| D、a>1或a<0 |
下列求导正确的是( )
A、y=
| ||||
| B、y=2x,则y′=2xln2 | ||||
| C、y=ex?cosx,则y′=ex?(-sinx) | ||||
D、y=
|
已知函数f(x)=
x3-
x2+cx+d有极值,则c的取值范围为( )
| 1 |
| 3 |
| 1 |
| 2 |
A、c<
| ||
B、c≤
| ||
C、c≥
| ||
D、c>
|
函数f(x)=ax3+bx2+cx+d(a≠0,x∈R)有极值点,则( )
| A、b2≤3ac | B、b2≥3ac | C、b2<3ac | D、b2>3ac |
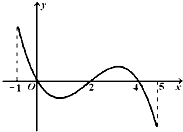 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f'(x)的图象如图所示.下列关于f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f'(x)的图象如图所示.下列关于f(x)的命题: