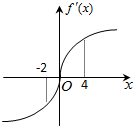
 已知定义在R上的函数f(x)满足f(4)=f(-2)=1,f′(x)为f(x)的导函数,且导函数y=f′(x)的图象如图所示.则不等式f(x)<1的解集是( )
已知定义在R上的函数f(x)满足f(4)=f(-2)=1,f′(x)为f(x)的导函数,且导函数y=f′(x)的图象如图所示.则不等式f(x)<1的解集是( )| A、(-2,0) | B、(-2,4) | C、(0,4) | D、(-∞,-2)∪(4,+∞) |
若f(x)=ax3+x在区间[-1,1]上是单调递增的,则a的取值范围为( )
A、[-
| ||
| B、[0,+∞) | ||
C、[
| ||
| D、[1,+∞) |
 已知定义在R上的函数f(x)满足f(4)=f(-2)=1,f′(x)为f(x)的导函数,且导函数y=f′(x)的图象如图所示.则不等式f(x)<1的解集是( )
已知定义在R上的函数f(x)满足f(4)=f(-2)=1,f′(x)为f(x)的导函数,且导函数y=f′(x)的图象如图所示.则不等式f(x)<1的解集是( )| A、(-2,0) | B、(-2,4) | C、(0,4) | D、(-∞,-2)∪(4,+∞) |
A、[-
| ||
| B、[0,+∞) | ||
C、[
| ||
| D、[1,+∞) |