某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料
(I)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于25”的概率.
(II)请根据3月2日至3月4日的数据,求出y关于x的线性回归方程
=
x+
;
(III)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(II)所得的线性回归方程是否可靠?
0 31432 31440 31446 31450 31456 31458 31462 31468 31470 31476 31482 31486 31488 31492 31498 31500 31506 31510 31512 31516 31518 31522 31524 31526 31527 31528 31530 31531 31532 31534 31536 31540 31542 31546 31548 31552 31558 31560 31566 31570 31572 31576 31582 31588 31590 31596 31600 31602 31608 31612 31618 31626 266669
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 温差x(°C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
(II)请根据3月2日至3月4日的数据,求出y关于x的线性回归方程
 |
| y |
 |
| b |
 |
| a |
(III)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(II)所得的线性回归方程是否可靠?
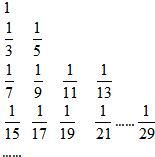 把数列
把数列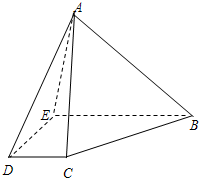 如图,在四棱锥A-BCDE中,底面BCDE是直角梯形,∠BED=90°,BE∥CD,AB=6,BC=5,
如图,在四棱锥A-BCDE中,底面BCDE是直角梯形,∠BED=90°,BE∥CD,AB=6,BC=5,