题目内容
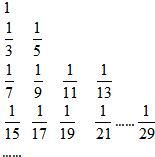 把数列{
把数列{| 1 |
| 2n-1 |
| 1 |
| 2009 |
分析:跟据第k行有2k-1个数知每行数的个数成等比数列,要求A(k,s),先求A(k,1),就必须求出前k-1行一共出现了多少个数,根据等比数列求和公式可求,而由
可知,每一行数的分母成等差数列,可求A(k,s),令k=5,s=12,可求A(5,12)
| 1 |
| 2n-1 |
解答:解:由第k行有2k-1个数,知每一行数的个数构成等比数列,首项是1,公比是2,
∴前k-1行共有
=2k-1-1个数,
∴第k行第一个数是A(k,1)=
=
,
∴A(k,s)=
,
∴A(5,12)=
;
由
=
,
得2k-1+2s-2=2009,s≤2k-1,
解得k=10,s=494.
故答案为
;10,494.
∴前k-1行共有
| 1-2k-1 |
| 1-2 |
∴第k行第一个数是A(k,1)=
| 1 |
| 2•2k-1-1 |
| 1 |
| 2k-1 |
∴A(k,s)=
| 1 |
| 2k-1 +2(s-1) |
∴A(5,12)=
| 1 |
| 53 |
由
| 1 |
| 2k-1 +2(s-1) |
| 1 |
| 2009 |
得2k-1+2s-2=2009,s≤2k-1,
解得k=10,s=494.
故答案为
| 1 |
| 53 |
点评:考查数列的性质和应用,解题是注意公式的灵活应用,此题是以一个数阵形式呈现的,考查观察、分析、归纳、解决问题的能力,属中档题.

练习册系列答案
相关题目
 把数列
把数列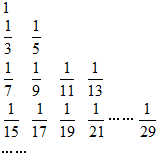 把数列
把数列 (2008•青浦区一模)把数列
(2008•青浦区一模)把数列 (2012•东城区模拟)把数列
(2012•东城区模拟)把数列