已知椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:
则C1、C2的标准方程分别为 、 .
| C1 | C2 | |||||||||
| x | 2 |
|
4 | 3 | ||||||
| y | 0 |
|
4 | -2
| ||||||
设F1、F2是双曲线x2-
=1的左、右两个焦点,若双曲线右支上存在一点P,使(
+
) •
=0(O为坐标原点)且|PF1|=λ|PF2|,则λ的值为( )
| y2 |
| 4 |
| OP |
| OF2 |
| F2P |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
定义在(0,+∞)上的可导函数f(x)满足f′(x)•x<f(x)且f(2)=0则
<0的解集为( )
| f(x) |
| x |
| A、(0,2) |
| B、(0,2)∪(2,+∞) |
| C、(2,+∞) |
| D、∅ |
从点A(2,-1,7)沿向量
=(8,9,-12)的方向取线段长|
|=34,则B点坐标为( )
| a |
| AB |
| A、(-9,-7,7) |
| B、(18,17,-17) |
| C、(9,7,-7) |
| D、(-14,-19,31) |
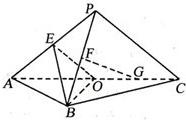 如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E、F、O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E、F、O分别为PA,PB,AC的中点,AC=16,PA=PC=10.