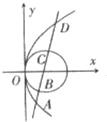
 如图抛物线C1:y2=2px和圆C2:(x-
如图抛物线C1:y2=2px和圆C2:(x-| p |
| 2 |
| p2 |
| 4 |
| AB |
| CD |
A、
| ||
B、
| ||
C、
| ||
| D、P2 |
已知椭圆
+
=1(a>0,b>0),A是椭圆长轴的一个端点,B是椭圆短轴的一个端点,F为椭圆的一个焦点.若AB⊥BF,则该椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图抛物线C1:y2=2px和圆C2:(x-
如图抛物线C1:y2=2px和圆C2:(x-| p |
| 2 |
| p2 |
| 4 |
| AB |
| CD |
A、
| ||
B、
| ||
C、
| ||
| D、P2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|