Question

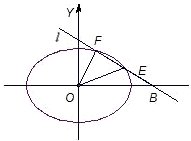已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的长轴长为2

2

，离心率e=

2

2

．
（1）求椭圆C的标准方程；
（2）若过点B（2，0）的直线l（斜率不等于零）与椭圆C交于不同的两点E、F（E在B、F之间），且△OBE与△OBF的面积之比为

1

2

，求直线l的方程．

Answer 1

分析：（1）设椭圆的标准方程，根据离心率求得a和c的关系，根据长轴长求得a，进而求得c，则b可求的，椭圆的方程可得．
（2）设直线l方程，与椭圆方程联立消去x，根据判别式大于0气度而m的一个范围，设E（x₁，y₁），F（x₂，y₂）利用韦达定理可分别表示出y₁y₂和y₁+y₂，根据三角形面积之比求得

|BE|

|BF|

=

1

2

由此可知，

BF

=2

BE

，即y₂=2y₁．代入y₁y₂和y₁+y₂中，进而求得m的范围．

解答：解：（1）椭圆C的方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，
由已知得

e= c a = 2 2 2a=2 2 a2=b2+c2

，
解得a=

2

，b =1，c=1，
∴所求椭圆的方程为

x2

2

+y2=1，
（2）由题意知l的斜率存在且不为零，
设l方程为x=my+2（m≠0）①，代入

x2

2

+y2=1，整理得（m²+2）y²+4my+2=0，由△＞0得m²＞2．
设E（x₁，y₁），F（x₂，y₂），则

y1+y2= -4m m2+2 y1y2= 2 m2+2

=2 ②
由已知，

S△OBE

S△OBF

=

1

2

，则

|BE|

|BF|

=

1

2

，
由此可知，

BF

=2

BE

，即y₂=2y₁．
代入 ②得，

3y1= -4m m2+2 2y12= 2 m2+2

，消去y₁得

2

9

•

16m2

(m2+2)2

=

2

m2+2

，
解得，m2=

18

7

，满足m²＞2．
即m=±

3 14

7

．
所以，所求直线l的方程7x-3

14

y-14=0或7x+3

14

y-14=0．

点评：本题主要考查了直线与圆锥曲线的综合问题．应充分挖掘题目的隐含条件，寻找量与量间的关系灵活转化，往往就能事半功倍．