题目内容
已知抛物线的焦点F在y轴上,抛物线上一点A(a,4)到准线的距离是5,过点F的直线与抛物线交于M,N两点,过M,N两点分别作抛物线的切线,这两条切线的交点为T.(I)求抛物线的标准方程;
(II)求
| FT |
| MN |
(III)求证:|
| FT |
| MF |
| NF |
分析:(I)先根据题意设出抛物线的方程,再结合点A到抛物线准线的距离可求出p的值,进而可得到抛物线的标准方程.
(II)先求出F的坐标,然后设出直线MN的方程,联立直线与抛物线消去y得到关于x的一元二次方程,表示出两根之和与两根之积,然后表示出
,再对x2=4y进行求导,表示出切线MT、NT的方程后联立解出交点T的坐标,得到
的坐标表示,最后使
•
运算等于0即可.
(III)根据(II)中
的坐标求出|
|2,再结合抛物线的定义课得到|
|=y1+1,|
|=y2+1.,再由|
|•|
|=(y1+1)(y2+1)并将直线方程y=kx+1代入,结合(II)中的两根之和与两根之积可得到|
|2=|
|•|
|.得证.
(II)先求出F的坐标,然后设出直线MN的方程,联立直线与抛物线消去y得到关于x的一元二次方程,表示出两根之和与两根之积,然后表示出
| MN |
| FT |
| FT |
| MN |
(III)根据(II)中
| FT |
| FT |
| MF |
| NF |
| MF |
| NF |
| FT |
| MF |
| NF |
解答:(I)解:由题意可设抛物线的方程为x2=2py(p≠0).
因为点A(a,4)在抛物线上,所以p>0.
又点A(a,4)到抛物线准线的距离是5,所以
+4=5,可得p=2.
所以抛物线的标准方程为x2=4y.
(II)解:点F为抛物线的焦点,则F(0,1).
依题意可知直线MN不与x轴垂直,
所以设直线MN的方程为y=kx+1.由
得x2-4kx-4=0.
因为MN过焦点F,所以判别式大于零.
设M(x1,y1),N(x2,y2).
则x1+x2=4k,x1x2=-4.
=(x2-x1,y2-y1)=(x2-x1,k(x2-x1)).
由于x2=4y,所以y′=
x.
切线MT的方程为y-y1=
x1(x-x1),①
切线NT的方程为y-y2=
x2(x-x2).②
由①,②,得T(
,
)
则
=T(
,
-1)=(2k,-2)
所以
•
=0.
(III)证明:|
|2=(2k)2+(-2)2=4k2+4.
由抛物线的定义知|
|=y1+1,|
|=y2+1.
则|
|•|
|=(y1+1)(y2+1)=(kx1+2)(kx2+2)
=k2x1x2+2k(x1+x2)+4=4k2+4.
所以|
|2=|
|•|
|.
即|
|是|
|和|
|的等比中项.
因为点A(a,4)在抛物线上,所以p>0.
又点A(a,4)到抛物线准线的距离是5,所以
| p |
| 2 |
所以抛物线的标准方程为x2=4y.
(II)解:点F为抛物线的焦点,则F(0,1).
依题意可知直线MN不与x轴垂直,
所以设直线MN的方程为y=kx+1.由
|
因为MN过焦点F,所以判别式大于零.
设M(x1,y1),N(x2,y2).
则x1+x2=4k,x1x2=-4.
| MN |
由于x2=4y,所以y′=
| 1 |
| 2 |
切线MT的方程为y-y1=
| 1 |
| 2 |
切线NT的方程为y-y2=
| 1 |
| 2 |
由①,②,得T(
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
则
| FT |
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
所以
| FT |
| MN |
(III)证明:|
| FT |
由抛物线的定义知|
| MF |
| NF |
则|
| MF |
| NF |
=k2x1x2+2k(x1+x2)+4=4k2+4.
所以|
| FT |
| MF |
| NF |
即|
| FT |
| MF |
| NF |
点评:本土主要考查直线与抛物线的综合问题以及向量的运算.直线与圆锥曲线是高考的重点问题,常以压轴题的形式出现.

练习册系列答案
相关题目
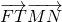 的值;
的值;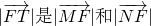 的等比中项.
的等比中项.