若抛物线y2=2px(p>0)的焦点在圆x2+y2+2x-3=0上,则p=( )
A、
| ||
| B、1 | ||
| C、2 | ||
| D、3 |
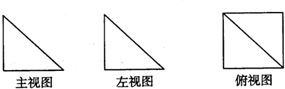 下图是一个空间几何体的主视图(正视图),左视图、俯视图,如果直角三角形边长均为1,那么这个几何体的侧面积为( )
下图是一个空间几何体的主视图(正视图),左视图、俯视图,如果直角三角形边长均为1,那么这个几何体的侧面积为( )A、2+2
| ||
B、1+2
| ||
C、2+
| ||
D、1+
|
 如图,是我市甲乙两地五月上旬日平均气温的统计图,则甲乙两地这十天的日平均气温的平均数
如图,是我市甲乙两地五月上旬日平均气温的统计图,则甲乙两地这十天的日平均气温的平均数. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
A、
| ||
| B、1 | ||
| C、2 | ||
| D、3 |
 下图是一个空间几何体的主视图(正视图),左视图、俯视图,如果直角三角形边长均为1,那么这个几何体的侧面积为( )
下图是一个空间几何体的主视图(正视图),左视图、俯视图,如果直角三角形边长均为1,那么这个几何体的侧面积为( )A、2+2
| ||
B、1+2
| ||
C、2+
| ||
D、1+
|
 如图,是我市甲乙两地五月上旬日平均气温的统计图,则甲乙两地这十天的日平均气温的平均数
如图,是我市甲乙两地五月上旬日平均气温的统计图,则甲乙两地这十天的日平均气温的平均数. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|