题目内容
观察下列式子：1+| 1 |
| 22 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20112 |
分析：由已知中，1+
＜
，1+
+
＜
，1+
+
+
＜
，…，观察分析不等式两边数的变化趋势，归纳其中规律后，推断出1+
+
+
+…+
＜
，将n=2011代入得到答案．
| 1 |
| 22 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| n2 |
| 2n-1 |
| 2 |
解答：解：由已知中的式子：
1+
＜
=
，
1+
+
＜
=
，
1+
+
+
＜
=
，
…，
我们可以推断
1+
+
+
+…+
＜
故1+
+
+
+…+
＜
=
故答案为：
1+
| 1 |
| 22 |
| 3 |
| 2 |
| 2×2-1 |
| 2 |
1+
| 1 |
| 22 |
| 1 |
| 23 |
| 5 |
| 3 |
| 2×3-1 |
| 3 |
1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
| 2×4-1 |
| 4 |
…，
我们可以推断
1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| n2 |
| 2n-1 |
| 2 |
故1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20112 |
| 2×2011-1 |
| 2011 |
| 4021 |
| 2011 |
故答案为：
| 4021 |
| 2011 |
点评：本题考查的知识点是归纳推理，其中根据已知的不等式，推断出1+
+
+
+…+
＜
是解答本题的关键．
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| n2 |
| 2n-1 |
| 2 |
练习册系列答案
阅读快车系列答案
相关题目
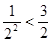,1+
＜
,1+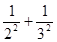
,…
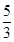,1+
,1+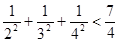
,…,由此猜想一个一般性的结论，并加以证明.