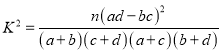【题目】对于函数，下列个结论正确的是__________（把你认为正确的答案全部写上）．

（1）任取，都有；

（2）函数在上单调递增；

（3），对一切恒成立；

（4）函数有个零点；

（5）若关于的方程有且只有两个不同的实根，，则.

①在某项测量中，测量结果服从正态分布，若在内取值范围概率为，则在内取值的概率为；

②若，为实数，则“”是“”的充分而不必要条件；

③已知命题，，则是：

，；

④中，“角，，成等差数列”是“”的充分不必要条件；其中，所有真命题的个数是（ ）

A. 个 B. 个 C. 个 D. 个

【题目】如图，菱形ABCD与正三角形BCE的边长均为2，且平面ABCD⊥平面BCE，平面ABCD，．

(I)求证：平面ABCD；

(II)求证：平面ACF⊥平面BDF．

①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形内角和是 归纳出所有三角形的内角和都是;③由,满足,,推出是奇函数;④三角形内角和是,四边形内角和是,五边形内角和是,由此得凸多边形内角和是.

A. ①②B. ①③④C. ①②④D. ②④

【题目】“双十一”已经成为网民们的网购狂欢节，某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查，用随机抽样的方法抽取了100人，其消费金额 (百元)的频率分布直方图如图所示：

(1)求网民消费金额的平均值和中位数；

(2)把下表中空格里的数填上，能否有的把握认为网购消费与性别有关；

附表：

.

（1）；（2）；（3）；（4）．

【题目】从年月份，某市街头出现共享单车，到月份，根据统计，市区所有人骑行过共享单车的人数已占，骑行过共享单车的人数中，有是大学生（含大中专及高职），该市区人口按万计算，大学生人数约万人.

（1）任选出一名大学生，求他（她）骑行过共享单车的概率；

（2）随单车投放数量增加，乱停乱放成为城市管理的问题，以下是累计投放单车数量与乱停乱放单车数量之间的关系图表：

①计算关于的线性回归方程（其中精确到值保留三位有效数字），并预测当时，单车乱停乱放的数量；

②已知该市共有五个区，其中有两个区的单车乱停乱放数量超过标准.在“双创”活动中，检查组随机抽取三个区调查单车乱停乱放数量， 表示“单车乱停乱放数量超过标准的区的个数”，求的分布列和数学期望.

参考公式和数据：回归直线方程中的斜率和截距的最小二乘法估计公式分别为 .

【题目】甲、乙两人投篮命中的概率分别为与，各自相互独立.现两人做投篮游戏，共比赛3局，每局每人各投一球.

（1）求比赛结束后甲的进球数比乙的进球数多1的概率；

（2）设表示比赛结束后甲、乙两人进球数的差的绝对值，求的概率分布和数学期望.

①过E，F，G三点作正方体的截面，所得截面为正六边形；

②B1D1∥平面EFG；

③BD1⊥平面ACB1；

④异面直线EF与BD1所成角的正切值为；

⑤四面体ACB1D1的体积等于a3

【题目】设函数.

（1）讨论函数的单调性；

（2）若函数在时恒成立，求实数的取值范围；

（3）若函数，求证：函数的极大值小于1.