题目内容
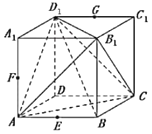
【题目】已知正方体ABCD-A1B1C1D1的棱长为a,点E,F,G分别为棱AB,AA1,C1D1的中点.下列结论中,正确结论的序号是______.
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②B1D1∥平面EFG;
③BD1⊥平面ACB1;
④异面直线EF与BD1所成角的正切值为![]() ;
;
⑤四面体ACB1D1的体积等于![]() a3
a3
【答案】①③④
【解析】
根据公理3,作截面可知①正确;根据直线与平面的位置关系可知②不正确;根据线面垂直的判定定理可知③正确;根据异面直线所成的角的定义求得异面直线EF与BD1的夹角的正切值为![]() ,可知④正确;用正方体体积减去四个正三棱锥的体积可知⑤不正确.
,可知④正确;用正方体体积减去四个正三棱锥的体积可知⑤不正确.
解:延长EF分别与B1A1,B1B的延长线交于N,Q,连接GN交A1D1于H,
设HG与B1C1的延长线交于P,连接PQ交CC1于I,交BC于M,
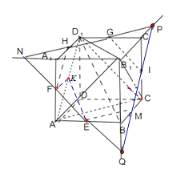
连FH,HG,GI,IM,ME,则截面六边形EFHGIM为正六边形,故①正确;
B1D1与HG相交,故B1D1与平面 EFG相交,所以②不正确;
∵BD1⊥AC,BD1⊥B1C,且AC与B1C相交,所以BD1⊥平面ACB1,故③正确;
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
所以![]() 就是异面直线EF与BD1的夹角,
就是异面直线EF与BD1的夹角,
设正方体的边长为![]() ,可得:
,可得:![]() ,
,![]() ,
,![]() ,
,
所以![]() 是直接三角形.可得:
是直接三角形.可得:![]() .
.
可得异面直线EF与BD1的夹角的正切值为![]() ,故④正确;
,故④正确;
四面体ACB1D1的体积等于正方体的体积减去四个正三棱锥的体积,
即为![]() ,故⑤不正确.
,故⑤不正确.
故答案为:①③④

练习册系列答案
相关题目