Question

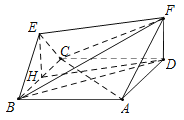
【题目】如图，菱形ABCD与正三角形BCE的边长均为2，且平面ABCD⊥平面BCE，平面ABCD，．

(I)求证：平面ABCD；

(II)求证：平面ACF⊥平面BDF．

Answer 1

【答案】（Ⅰ）见解析;（Ⅱ）见解析.

【解析】

(1)添加辅助线，通过证明线线平行来证明线面平行.

(2) 通过证明线面垂直面，来证明面面.

（Ⅰ）证明：如图，过点作于，连接，∴．

∵平面⊥平面，平面，

平面平面 ，

∴⊥平面，

又∵⊥平面，，

∴，.

∴四边形为平行四边形．

∴.

∵平面，平面，

∴平面．

（Ⅱ）证明：面，，又四边形是菱形，

，又，面，

又面，从而面面．

点晴：本题考查的是空间线面的平行和垂直关系.第一问要考查的是线面平行，通过先证明，得四边形为平行四边形．证得，可得平面，这里对于线面平行的条件平面，平面要写全;第二问中通过先证明面，再结合面，从而面面．