题目内容
【题目】作出下列函数的大致图像,并写出函数的单调区间和值域.
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【答案】(1)增区间:![]() ,值域:R;
,值域:R;
(2)增区间:![]() 和
和![]() ,减区间:
,减区间:![]() ,值域:
,值域:![]() ;
;
(3)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ;
;
(4)减区间:![]() 和
和![]() ,增区间:
,增区间:![]() 和
和![]() ,值域:
,值域:![]() ,大致图像见解析
,大致图像见解析
【解析】
(1)由![]() ,由对称性即可作出图像,结合图像即可求出单调性、值域.
,由对称性即可作出图像,结合图像即可求出单调性、值域.
(2)将函数化为![]() ,利用幂函数的图像,由平移即可作出图像,结合图像即可求出单调性、值域.
,利用幂函数的图像,由平移即可作出图像,结合图像即可求出单调性、值域.
(3)由![]() ,通过图像的翻折变化即可作出图像,结合图像即可求出单调性、值域.
,通过图像的翻折变化即可作出图像,结合图像即可求出单调性、值域.
(4)由![]() ,去绝对值,描点即可作出大致图像,结合图像即可求出单调性、值域.
,去绝对值,描点即可作出大致图像,结合图像即可求出单调性、值域.
(1)函数![]() 的图象如图所示:
的图象如图所示:
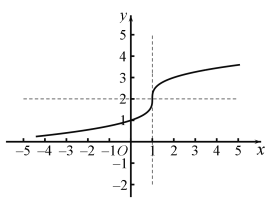
函数在![]() 上为增函数,值域:
上为增函数,值域:![]() .
.
(2)![]() ,图象如图所示:
,图象如图所示:
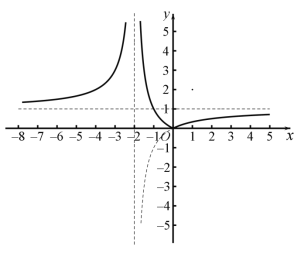
函数在![]() 和
和![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
值域为:![]() .
.
(3)![]() ,图象如图所示:
,图象如图所示:
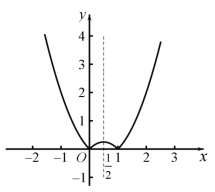
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数.
为增函数.
值域为:![]() ;
;
(4)![]()
,
函数在![]() 和
和![]() 为减函数,在
为减函数,在![]() 和
和![]() 为增函数,
为增函数,
值域为:![]() .
.

练习册系列答案
相关题目